Find the perimeter

Moderate
0/80
profile
Contributed by
3 upvotes
Asked in companies
AdobeBloomsbury PublishingTower Research Capital

Problem statement

You are given a map of an island. Your task is to find the perimeter of the island. The map is represented by a binary grid where ‘0’ represents water, and ‘1’ represents the land.

Note: 
There is only one island and water surrounding it. There are no lakes, i.e., all the water is connected. Each edge of the land is 1 unit.
For example:
You are given map = [[0, 0, 0, 0, 0],
                     [0, 0, 1, 0, 0],
                     [0, 1, 1, 1, 0],
                     [0, 0, 1, 0, 0]]

You are given the map as:

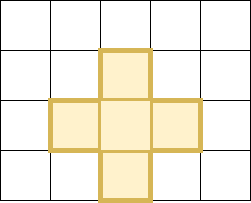
sample1

Here, it can be clearly seen the perimeter of the island is 12. Hence the answer is 12.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains a single integer ‘T’, representing the number of test cases.

The first line of each test case contains two space-separated integers, ‘N’ and ‘M’, representing the number of rows and columns in the given map.

The following ‘N’ lines of each test case contain ‘M’ space-separated integers representing each row of the map.
Output Format: 
For each test case print a single integer value representing the perimeter of the given island in the map.

Print the output of each test case in a separate line.
Constraints: 
1 <= T <= 10
1 <= N, M <= 10^3
map[i][j] == 1 or 0

Time Limit: 1 sec
Note: 
You do not need to print anything. It has already been taken care of. Just implement the function.
Sample Input 1: 
2
4 5
0 0 0 0 0
0 0 1 0 0
0 1 1 1 0
0 0 1 0 0
2 3
0 1 0
0 0 0
Sample Output 1:
12
4
Explanation:
For the first test case, map = [[0, 0, 0, 0, 0],
                                [0, 0, 1, 0, 0],
                                [0, 1, 1, 1, 0],
                                [0, 0, 1, 0, 0]]
You are given the map as:

sample1

Here, it can be clearly seen the perimeter of the island is 12. Hence the answer is 12


For the second test case, map = [[0, 1, 0],
                                 [0, 0, 0]]
You are given the map as:

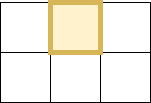
sample2

Here, it can be clearly seen the perimeter of the island is 4. Hence the answer is 4.
Sample Input 2:
2 
3 3
0 0 0
0 1 1
0 1 1
1 1 
0
Sample Output 2:
8
0
Hint

Count the number of ‘1’ and its neighbours.

Approaches (1)
Iterative Approach

In this approach, we will iterate over the given ‘map’ matrix count the number of ‘1’. If any ‘1’ has a right or down neighbour land cell we count them separately. Since each ‘1’ can add a maximum of 4 towards the perimeter and if there exists a neighbour land cell we subtract 2 from the overall perimeter. 

Hence the final perimeter is 4* number of ‘1’ - 2* no. of neighbours.

 

Algorithm:

  • Set count and neighbours as 0
  • Iterate row through the map 
    • Iterate col through map[row]
      • If map[row][col] is not equal to 1 continue the loop.
      • Increase count by 1
      • If row is less than length of map - 1 and map[row + 1][col] is equal to 1
        • Increase neighbours by 1
      • If col is less than length of map[row] - 1 and map[row][col + 1] is equal to 1
        • Increase neighbours by 1
  • Set ans as 4* count
  • Decrease ans by 2* neighbours
  • Finally, return ans
Time Complexity

O(N*M), Where N and M are the number of rows and columns in the map.

 

We are iterating through the whole map once which will cost O(N*M) time. Hence the final time complexity is O(N*M).

Space Complexity

O(1),

 

We are only using constant space in the algorithm, Hence the final space complexity is O(1).

Code Solution
(100% EXP penalty)
Find the perimeter
Full screen
Console