Fix BST

Hard
0/120
Average time to solve is 45m
profile
Contributed by
27 upvotes
Asked in companies
MicrosoftSquadstackOYO

Problem statement

You have been given a Binary Search Tree of 'N' nodes, where exactly two nodes of the same tree were swapped by mistake.


Your task is to restore or fix the BST, without changing its structure and return the root of the corrected BST.


Note:

Given BST will not contain duplicates.


Example 
A Binary Search Tree (BST) whose 2 nodes have been swapped is shown below.

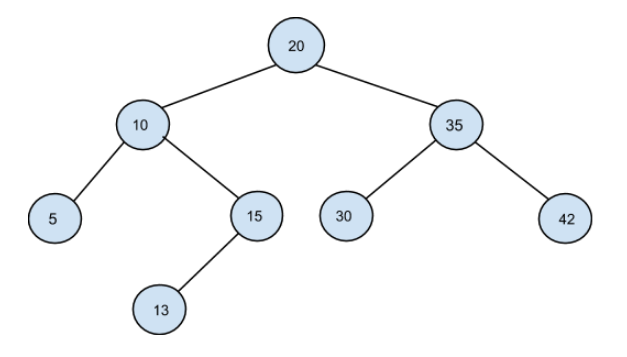
example

After swapping the incorrect nodes:

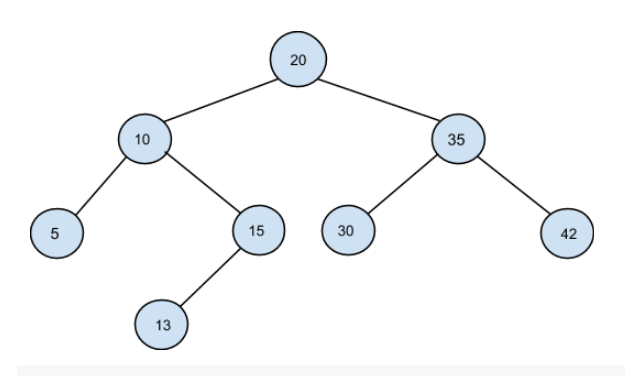
example

Follow Up 
Can you do this without using any extra space?
Detailed explanation ( Input/output format, Notes, Images )
Input Format 
The first line contains elements in the level order form. The input consists of values of nodes separated by a single space in a single line. In case a node is null, we take -1 on its place.
Example : 
The input for the tree is depicted in the below image:

BT - 2

1 3 8 5 2 7 -1 -1 -1 -1 -1 -1 -1
Explanation : 
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 3
Right child of 1 = 8

Level 3 :
Left child of 3 = 5
Right child of 3 = 2
Left child of 8 =7
Right child of 8 =  null (-1)


Level 4 :
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 2 = null (-1)
Right child of 2 = null (-1)
Left child of 7 = null (-1)
Right child of 7 = null (-1)

1
3 8
5 2 7 -1
-1 -1 -1 -1 -1 -1
Note : 
1. The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

2. The input ends when all nodes at the last level are null(-1).

3. The above format was just to provide clarity on how the input is formed for a given tree. The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 3 8 5 2 7 -1 -1 -1 -1 -1 -1 -1
Output Format: 
The output contains the 'N' single space-separated level order traversal of the restored tree.
Note: 
You don’t have to print anything, it has already been taken care of. Just implement the function.
Sample Input 1:
1 5 -1 -1 3 -1 -1
Sample Output 1:
5 1 3
Explanation of sample input 1:
5 cannot be the left child of 1 as 5 > 1. Swapping 5 and 1 will result in a valid BST.
Sample Input 2:
3 1 4 -1 -1 2 -1 -1 -1
Sample Output 2:
2 1 4 3
Constraints :
1 <= 'N' <= 10^3
0 <= 'data' <= 10^5     

where 'N' is the number of nodes and 'data' denotes the node value of the binary tree nodes.

Time limit: 1 sec
Hint

Can you do this by storing the inorder traversal of the tree?

Approaches (4)
Sorting based Approach

The steps are as follows:

 

  1. Maintain an array, say ‘INORDERTRAVERSAL’, and store the inorder traversal of the given BST in this array.
  2. Now sort the ‘INORDERTRAVERSAL’ array.
  3. After sorting, we have the valid BST’s inorder traversal.
  4. Again, traverse the tree in inorder fashion and keep updating the value at each node according to the ‘inOrderTraversal’ array.

 

Algorithm for storing inorder traversal :

 

void inorder('ROOT', ‘INORDERTRAVERSAL’)

  1. Until all the nodes are traversed
    • Recursively traverse the left subtree.
    • Add the current node’s value to the ‘INORDERTRAVERSAL’ array.
    • Recursively traverse the right subtree.
Time Complexity

O(N * log(N)) where ‘N’ is the number of nodes in the given BST.

 

Since we are traversing the tree for storing the inorder traversal and then we are sorting the array. Storing in order traversal and the final process of updating the values of the nodes can be done in O(N) time. Sorting the array takes O(N * log(N)) time and thus, the final time complexity is O(N + N * log(N) + N) = O(N * log(N)). 

Space Complexity

O(N), where ‘N’ is the number of nodes of the given BST.

 

Since we are storing the value of every node of the tree in the array. Thus, the final space complexity is O(N).  

Code Solution
(100% EXP penalty)
Fix BST
Full screen
Console