Gold mine problem

Moderate
0/80
Average time to solve is 35m
profile
Contributed by
24 upvotes
Asked in companies
SamsungGoldman SachsAmazon

Problem statement

You have been given a gold mine represented by a 2-d matrix of size ('N' * 'M') 'N' rows and 'M' columns. Each field/cell in this mine contains a positive integer, the amount of gold in kgs.

Initially, the miner is at the first column but can be at any row.

He can move only right, right up, or right down. That is from a given cell and the miner can move to the cell diagonally up towards the right or right or diagonally down towards the right.

Find out the maximum amount of gold he can collect.

Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains an integer 'T’, which denotes the number of Test cases.
The next '2' * 'T' lines represent the ‘T’ test cases.

The first line of each test case contains two single space-separated integers 'N' and 'M' denoting the size of the gold mine.

The second line of each test case contains 'N' * 'M' space-separated integers representing the gold mine.
Output Format: 
For each test case print an integer 'X'  denoting the maximum amount of gold collected.

Output for each test case will be printed in a separate line.
Note: 
You are not required to print the output, it has already been taken care of. Just implement the function.
Constraints: 
1 <= T <= 10
1 <= N <= 100
1 <= M <= 100
0 <= gold at each cell <= 10^5 

Time Limit: 1 sec
Sample Input 1
2  
4 4
10 33 13 15 22 21 4 1 5 0 2 3 0 6 14 2
3 3
1 3 3 2 1 4 0 6 4
Sample Output 1:
83 
12
Explanation For The Sample Output 1:
Here we have 2 test cases in total.

Test case 1:

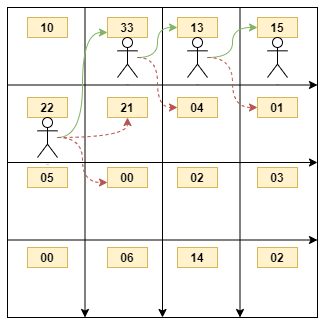
Test case

Here miner starts from row 2 of the first column and collects gold of 22 kgs. Then he tries diagonally up towards the right(33 kgs), straight right(21 kgs), and diagonally down towards the right(00 kgs) and chooses the right upper diagonal cell. 
Hence the total gold with miner is 22+33=55 kgs. Going forward, miner chose the straight right path with 13 kgs and 15 kgs. Hence the maximum value of gold collected by the miner is 83 kgs. 
There is no other path starting from any row of the first column, which gives the miner more gold than 83kgs.

Test case 2: 
The mine has 3 rows, miner chose the second row, the cell with 2 kgs. Going forward, the miner chose to go diagonally down towards the right (2+6=8 kgs). Further miner goes straight right to the cell with the gold of 4 kgs. Hence the maximum value of gold collected by the miner is (2+6+8) 12 kgs.
Sample Input 2:
2
3 3
1 3 4 8 9 8 7 5 6
1 1
2
Sample Output 2:
25
2
Hint

Think of a recursive solution.

Approaches (3)
Recursive Solution
  • The miner can start from any row of the first column, hence we will be calling our recursive function from all the rows of column 1 as the starting block/cell.
  • In the recursive function, a miner can move in three particular directions:
    • Upper right diagonal -> ('R' - 1,'C' + 1)
    • Straight right -> ('R','C')
    • Lower right diagonal -> ('R' + 1, ‘C’)
  • Hence each function call will be representing/returning the addition of gold at that cell and the maximum of gold collected by choosing the best possible path ahead.
  • The base condition of the recursive function would be :
    • When column reaches its limit -> ('C' == 'M;)
    • When row is negative -> ('R' < 0)
    • When row reaches its limit -> ('R' == ‘N’ )

 

Finally, in the end, we will be getting maximum of gold collected starting from each row of the first column in the main function. We will be returning maximum of all those amounts.

Time Complexity

O(3 ^ (N * M)). Here, ‘N’ denotes the number of rows of mine and ‘M’ denotes the number of columns of the mine.

 

Each recursive function will further call 3 new recursive functions for each cell. Hence the overall complexity will be O(3 ^ (N * M)).

Space Complexity

O(M). Here, ‘M’ denotes the number of columns of the mine.

 

The size of the stack for the recursive function calls will be ‘M’. So the overall space complexity will be O(M)

Code Solution
(100% EXP penalty)
Gold mine problem
Full screen
Console