Graph Valid Tree

Moderate
0/80
Average time to solve is 30m
profile
Contributed by
12 upvotes
Asked in companies
alibabaIndeed

Problem statement

You are given N nodes labelled from 0 to N - 1 and a list of undirected edges( each edge is a pair of nodes). Your task is to find out if these edges make a valid tree. If they make a valid tree return true, else return false.

Tree is a special graph. It has the following properties.

• It is connected
• It has no cycle.

Example :

If n = 5 and if there are 4 edges i.e [ [0, 1], [0, 2], [0, 3], [1, 4]] so the graph formed will look like this:-


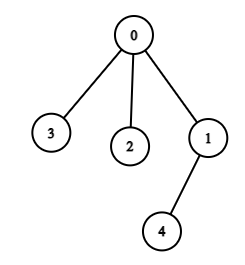
Here this graph is connected and it has no cycle so it is a tree.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line of input contains an integer T’ denoting the number of test cases to run. Then the test case follows.

The first line of each test contains an integer ‘N’ where N is the number of nodes.

The next line of each test case contains an integer ‘M’ where M is the number of edges.

Then the following m lines contain two space separated integers each representing the list of undirected edges.
Output Format : 
For each test case, print "True" if the graph is a valid tree otherwise print "False".
Note : 
You don’t have to take input or print anything. This already has been taken care of. Just implement the function.
Constraints : 
1 <= T <= 5
1 <= N <= 10^3
1 <= M <= 10^3
Sample Input 1 :
2
5
4
0 1
0 2
0 3
1 4
5
5
0 1
1 2
2 3
1 3
1 4
Sample Output 1 :
True
False
Explanation of sample input 1 :
Test case 1:

If n = 5, and k = 5 and undirected edges are [0, 1], [0, 2], [0, 3], [1, 4]. With these edges the graph will look like this:


Here there is no cycle and the graph is connected hence it is a tree.

Test case 2:

If n = 5 and k = 5 and the edges are [0, 1], [1, 2], [2, 3], [1, 3], [1, 4]. The graph will look like this:


Here there is a cycle between nodes 1,2 and 3. Hence this graph is not a tree.
Sample Input 2 :
2
5
5
0 1
0 2
1 3
3 2
2 4
4
3 
0 1
0 2
1 3
Sample Output 2 :
False
True
Hint

Check for the special properties of trees.

Approaches (1)
Depth First Search

For a graph being a tree, we have to check the following things

 

  1. Checking how many connected components are present in the graph, It can only be a tree if it has only one connected component
  2. Checking if it has a cycle or not.

 

Algorithm:

  • We will check connected components using Depth-first Search(DFS).
  • Start DFS from every unvisited node from 0 till N-1.
  • If we start DFS from zero and there is only one connected component, then all the nodes will get visited after completion of this DFS.
  • But if there is more than one connected component, then after visiting all the nodes reachable from zero, we will have to encounter and start from other unvisited nodes too.
  • Initialize a variable count=0 to store the count of connected components.
  • Iterate i from 0 to N-1, and a boolean array visited to store the status of visited and unvisited nodes.
    • If visited[i]==false then DFS(i), and increase  count  by 1.
  • If count > 1, then it can’t be a tree.
  • Else we have to check for a cycle.
  • For checking the cycle, start DFS from any node let say zero.
  • Visit all direct children of 0, and subsequently their children as well.
  • We are working with an undirected graph so a cycle is will be present if a node that is already visited in DFS is the direct children of some node we are currently are at.
  • If such a case exits our the cycle will be present. And the graph will not be a tree.
  • Otherwise, our graph is a tree.
Time Complexity

O(N) where N is the number of nodes.

 

We are performing DFS for N nodes hence time complexity will be O(N).

 

Space Complexity

 O (N)  where N is the number of nodes.

 

We are storing the status of visited nodes in an array of size N so the space complexity will be O(N).

Code Solution
(100% EXP penalty)
Graph Valid Tree
Full screen
Console