Interleaving Two Strings

Moderate
0/80
Average time to solve is 45m
profile
Contributed by
19 upvotes
Asked in companies
AppleFacebookAmazon

Problem statement

You are given three strings 'A', 'B' and 'C'. Check whether 'C' is formed by an interleaving of 'A' and 'B'.

'C' is said to be interleaving 'A' and 'B', if the length of 'C' is equal to the sum of the length of 'A' and length of 'B', all the characters of 'A' and 'B' are present in 'C' and the order of all these characters remains the same in all three strings.

For Example: 
If A = “aab”, 'B' = “abc”, 'C' = “aaabbc”
Here 'C' is an interleaving string of 'A' and 'B'. because 'C' contains all the characters of 'A' and 'B' and the order of all these characters is also the same in all three strings.

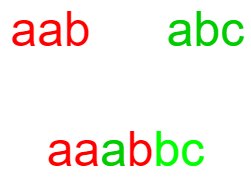
interleaving

If 'A' = “abc”, 'B' = “def”, 'C' = “abcdefg”
Here 'C' is not an interleaving string of 'A' and 'B'. 'B'ecause neither A nor 'B' contains the character ‘g’.
Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then, the T test cases follow.

The first and only line of each test case contains three strings 'A', 'B' and 'C' each separated by a single space.
Output format: 
For each test, print True, if 'C' is an interleaving string of 'A' and 'B, otherwise print False in a separate line.
Note: 
You do not need to print anything, it has already been taken care of. Just implement the given function.
'C'onstraints: 
1 <= T <= 10
1 <= |'A'|, |'B'| <= 150
1 <= |'C'| <= 300

where |A|, |'B'|, |'C'| denotes the length of string 'A', 'B' and 'C' respectively.   
All the characters of the strings 'A', 'B' and 'C' contain lowercase English letters only.

Time limit: 1 sec
Sample Input 1:
2
abdd fef abfddef
aab abc aabbc
Sample Output 1:
True
False
Explanation for sample 1:
For the first test case, all the characters of A and B are present in C, in the same order.
For the second case,'C' < ('A' + 'B').
Sample Input 2:
2
zxry qwr qwzxxryr
a a aa
Sample output 2:
False
True
Explanation for sample 2:
For the first test case, 'C' > ('A' + 'B').
For the second test case, all the characters of A and B are present in C in the same order.
Hint

Think of a brute force solution using recursion.

Approaches (4)
Brute-force

Approach:

In order to solve this problem, let us solve a smaller problem first. Let’s assume that the length of the string A and B is 1 and the length of the string C is 2. Now in order to check whether C is formed by interleaving A and B or not, we consider the last character of string C and if this character matches neither with the character of the string A nor with the character of string B, then we return false. But if it matches with any of the characters either from A or from B, we check the same for the other character in C. So, let's further expand this idea, for bigger problems. So, if the last character of C, matches with either the last character of A or B, we check recursively for the second last element and then the third last element and so on, until we finally reach the base case when all the strings eventually become empty.

 

Steps:

  1. We create a recursive function let’s say isInterleaveUtil and pass A, B, C, n1, n2, n3 as arguments, where n1,n2, and n3 are the length of A, B, and C.

bool isInterleaveUtil( A, B, C, n1, n2, n3):

  1. If all the strings become empty i.e n1,n2.and n3 become 0, then simply return true.
  2. If the length of C is not equal to (length of A + length of B),i.e  n1+n2 != n3 then we simply return false.
  3. If the last character of both A and B matches with the last character of C, then we check for both the cases i.e. retreating A by one character and B by one character i.e call isInterleaveUtil(A, B, C, n1-1, n2, n3-1) and isInterleaveUtil(A, B, C, n1, n2-1, n3-1), and return true, if either of them returns true.
  4. If the last character of C matches with the last character of A, but not with the last character of B, we move one character back in A and check recursively. I.e. call  isInterleaveUtil(A, B, C, n1-1, n2, n3-1);
  5. If the last character of C matches with the last character of B, but not with the last character of A, we move one character back in B and check recursively. I.e. call  isInterleaveUtil(A, B, C, n1, n2-1, n3-1).
  6. If the last character of C matches neither with the last character of A nor with the last character of B, then we simply return false.
Time Complexity

O(2^(N + M)), where N is the length of the string A and M is the length of string B.

 

In the worst case, for every character of the input strings A and B, there can be two choices. Hence, the time complexity will be O(2^(N + M)).

Space Complexity

O(N + M), where N is the length of the string A and M is the length of string B.

 

In the worst case, the size of stack for recursive calls can go upto (N + M). Hence the overall complexity will be O(N + M).

Code Solution
(100% EXP penalty)
Interleaving Two Strings
Full screen
Console