Invert a Binary Tree

Moderate
0/80
Average time to solve is 45m
46 upvotes
Asked in companies
AppleSamsungFreshworks

Problem statement

You are provided with a Binary Tree and one of its leaf nodes. You have to invert this binary tree. Inversion must be done by following all the below guidelines:

• The given leaf node becomes the root after the inversion.

• For a node (say, ‘x’) 
    ○ If there exists the left child that is not yet taken then this child must become the right child of ‘x’.
    ○ If the left child is already taken then the right child is still on the right side of ‘x’.

• The parent of ‘x’ must be the left child of ‘x’.

For Example:

Example-img01
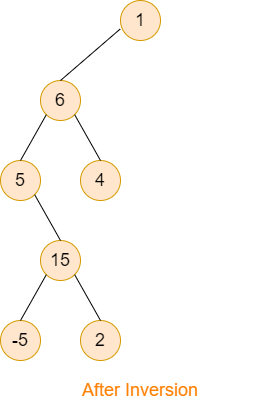
Example-img02

Consider the above binary tree (image- before inversion), if the given leaf node is ‘1’ then the binary tree after inversion becomes exactly the same as given in the image representing after inversion.

Note:

The given binary tree will only have distinct values of nodes.

Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains a single integer ‘T’ representing the number of test cases. 

The first line of each test case will contain a single TreeNode “leaf” which denotes one of the leaf nodes of the given binary tree.

The second line of each test case contains elements of the tree in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image would be :

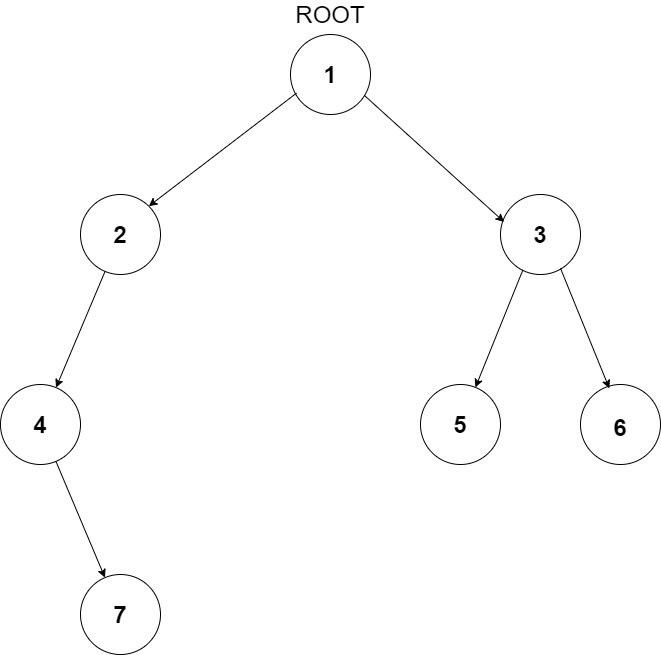
Example

1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :

Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null(-1).
Note : 
The above format was just to provide clarity on how the input is formed for a given tree. 
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format: 
For each test case, return the whole binary tree (according to the format as it has been given in the input) after considering the given leaf node as the new root node.

Output for every test case will be printed in a separate line.
Note: 
You don’t need to print anything; It has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 50
1 <= N <= 10000
-10^5 <= DATA <= 10^5
Leaf is one of the leaf nodes of the given binary tree.

Time limit: 1 sec
Sample Input 1:
1
1
5 6 15 4 1 -5 2 -1 -1 -1 -1 -1 -1 -1 -1
Sample Output 1:
1 6 -1 5 4 -1 15 -1 -1 -5 2 -1 -1 -1 -1
Explanation of sample input 1:
For the first test case, the explanation is provided in the description.
Sample Input 2:
2
2
1 2 3 -1 -1 -1 -1
3
1 2 -1 3 -1 -1 -1
Sample Output 2:
2 1 -1 -1 3 -1 -1
3 2 -1 1 -1 -1 -1
Explanation for sample input 2:
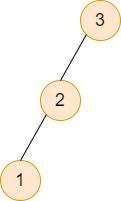
In the first test case, the inverted tree will look like this:

Explanation

In the second test case, the inverted tree will look like this:

Explanation

Hint

Can you think of a solution after finding the path that includes the given leaf node?

Approaches (1)
In-order Traversal

The basic idea is to first fill all the nodes (in a stack) that are present in a path whose leaf node is the given leaf node using In-order traversal. And, then keep removing nodes from the stack and attaching with the given leaf node according to the given guidelines.

 

We are using a helper function that takes the root of the given binary tree, a stack, and the given leaf node as input and returns a boolean that denotes whether this path includes the given leaf node or not (true if includes, otherwise false).

 

bool helper(TreeNode<int> *root, stack<TreeNode<int> *> &st, TreeNode<int> *leaf)

 

Where “ROOT” is the root of the given binary tree, “ST” is the stack that holds nodes present in the current path, and “LEAF” is the given leaf node.

 

The steps are as follows:

 

  1. In the “HELPER” function
    • Push the “ROOT” into the “ST”.
    • Check if the “ROOT” is a leaf Node.
      • Now, if “ROOT” is the given leaf node i.e “LEAF” then return true.
      • Else, pop out the node stored at the top of “ST” and return false.
    • Make a recursive call for the left subtree and if the result obtained is true then return true.
    • Similarly, do for the left subtree.
    • Pop-out the node stored at the top of “ST” and return false.
  2. In the given function
    • Check if the “ROOT” is NULL then return “ROOT”.
    • Make a stack named “ST” to store the nodes present in the current path.
    • Call the “HELPER” function by passing arguments as “ROOT”, “ST”, and “LEAF”.
    • Create a node named “NEW_ROOT” which holds the new root of the given binary tree. Set “NEW_ROOT” to the node stored at the top of “ST”.
    • Pop-out the node stored at the top of “ST”.
    • Create another node named “PARENT” that will hold the parent node. Initially set “PARENT” equal to “NEW_ROOT”.
    • Iterate while “ST” is not empty.
      • Pop-out the top node of “ST” and store in a node named “CUR_NODE”.
      • Now, check if the left of the “CUR_NODE” is “PARENT” then just set its left NULL and assign it to the left of “PARENT”.
      • Else, make its right child to its left child and then set the left child as NULL. And, finally, make this “CUR_NODE” the left child of “PARENT”.
      • Move “PARENT” ahead.
    • Return “NEW_ROOT”.
Time Complexity

O(N), where ‘N’ is the total number of nodes in the given binary tree.

 

Since in the “helper” function we are just traversing each node (takes O(N) time) and in the main function we are just removing every node that is stored in the stack that might go up to N in case of the skewed tree (takes O(N) time) and so the overall time complexity will be O(N).

Space Complexity

O(N), where ‘N’ is the total number of coins.

 

Since we are using extra space in the form of a stack that can take O(N) space in case of a skewed tree and so, the overall space complexity will be O(N).

Video Solution
Unlock at level 3
(75% EXP penalty)
Code Solution
(100% EXP penalty)
Invert a Binary Tree
Full screen
Console