Problem

Submissions

Hints & solutions

Discuss

Josephus

Moderate

0/80

Average time to solve is 30m

Contributed by

30 upvotes

Asked in companies

Problem statement

‘N’ people are standing in a circle numbered from ‘1’ to ‘N’ in clockwise order. First, the person numbered 1 will proceed in a clockwise direction and will skip K-1 persons including itself and will kill a Kth person. Now (K+1)th person from 1 will start and will kill the Kth person from itself.

You have to find the position of the last person surviving with respect to initial numbering.

Note:

A person can also kill himself.

Detailed explanation ( Input/output format, Notes, Images )

Input Format

The first line of input contains an integer ‘T’ denoting the number of test cases.

The first and only line of each test case contains two integers ‘N’ and ‘K’. Where ‘N’ is the total no of persons standing around circle and ‘K’  number indicates kth person is killed.

Output Format

For each test case, return a single integer denoting the position of the last person surviving.

Note:

You are not required to print the output explicitly, it has already been taken care of. Just implement the function.

Constraints

1 <= ’T’ <= 50
1 <= ’N’,’K’ <= 10^4

Time Limit: 1 sec

Sample Input 1

2
4 2 
7 3

Sample Output 1:

1
4
Explanation :-

For the first TestCase:-

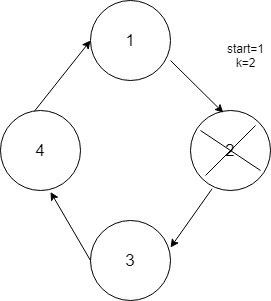
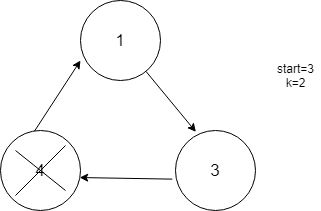
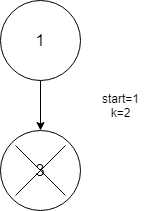
The position of the last person is 1.Hence ans is 1.
For the second case:-
The first starting point is 1 and 3 is killed.
The starting point is 4 and 6 is killed.
The starting point is 7 and 2 is killed.
The starting point is 4 and 7 is killed.
The starting point is 1 and 1 is killed.

Sample Input 2

2
5 6
3 6

Sample Output2

4 
1

Hint 1

Hint 2

Use Brute Force approach.

Approaches (2)

Approach 1

Approach 2

Brute Force

Approach:- The key id is to store all positions of a person in vector and remove all kth position from starting point in vector. After removing an element from the vector starting point is also changed.

Algorithm:

Store all the positions of persons in the index array.
Initially the starting position will be 0(since pos[0]=1).
Delete the element at position 'START1'= (START + K - 1) % N. Whereas ‘N’ is the size of the index array.
Now the starting position will be ‘START1’.
Repeat step3 until size of array becomes equal to 1.
Return the only element of index array.

Time Complexity

O(N^2), where ‘N’ is the number of persons.

We iterate every index in worse case in each iteration we delete element from the array which takes O(N) time. Hence time complexity is O(N^2).

Space Complexity

O(N), where ‘N’ is the number of persons.

Create an index array to store the positions of all persons.

(100% EXP penalty)

Josephus

Console