K Centers

Moderate
0/80
Average time to solve is 25m
profile
Contributed by
8 upvotes
Asked in companies
AmazonJaguar Land RoverWinZO

Problem statement

In Ninja Land there are ‘N’ cities numbered from 0 to ‘N’-1. The distance between each pair of cities is given by N * N matrix ‘DIST’ where ‘DIST[i][j]’ denotes the distance between city ‘i’ and ‘j’.

Ninja wants to select ‘K’ (‘K’ <= ‘N’) cities and install Coding Ninjas Server in these cities. He wants to select ‘K’ cities in such a way that the maximum distance of a city from the Coding Ninjas Server is minimized.

Can you help Ninja in finding this maximum distance if he selects ‘K’ cities optimally? You should return this distance.

Note : 
1. DIST[i][j] = DIST[j][i].
2. DIST[i][i] = 0.
Example : 
Consider that there are 4 cities i.e. ‘N’ = 4, and the distance between each pair of cities is given by the following matrix ‘DIST’:  
             [0, 10, 7, 6]
             [10, 0, 8, 5]
             [7, 8, 0, 12]
             [6, 5, 12, 0]

Graphically, cities can be represented as -:

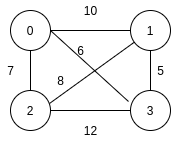
alt text

Assume Ninjas wants to install a server in 2 cities i.e ‘K’ = 2.  Then one optimal choice is to select cities 2 and 3.
After that, the minimum distance of city 0 from the server is  6  (i.e from city 2).
The minimum distance of city 1 from the server is 5  (i.e from city 3).
The minimum distance of cities 2 and 3 from the server is 0, as the server is installed in these cities.
Thus the maximum distance of the city from the server is max (6, 5, 0, 0) = 6.
So, we should return 6.
No selection of two cities can give a maximum distance which is less than 6.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line of input contains an integer ‘T’ denoting the number of test cases. then ‘T’ test cases follow.

The first line of each test case consists of two single space-separated integers ‘N’ and ‘K’ respectively representing the number of cities in Ninja Land and the number of cities where the server needs to be installed.

The next ‘N’ line follows in each test case. Each of these ‘N’ lines consists of ’N’ single space-separated integers. These ‘N’ lines together represent the matrix ‘DIST’.
Output Format : 
For each test case, print a single integer that represents the maximum distance of a city from the server when ‘K’ cities are selected optimally.

Print the output of each test case in a separate line.

Note :

You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints : 
1 <= T <= 50
1 <= N <= 15
1 <= K <= N
1 <= DIST[i][j] <= 10^9,  for i != j
DIST[i][j] = 0, for i = j

Time limit: 1 sec
Sample Input 1 :
2
1 1
0
4 2
0 10 7 6
10 0 8 5
7 8 0 12
6 5 12 0
Sample Output 1 :
0
6
Explanation Of Sample Input 1 :
Test case 1:
There is only 1 city i.e city 0, Ninja can install a server in it. As the distance of the city from itself is 0. So the answer will also be 0.

Test case 2:
See the problem statement for an explanation.
Sample Input 2 :
2
3 3
0 10 1
10 0 5
1 5 0
2 1
5 0
0 5
Sample Output 2 :
0
5
Hint

One by one try out all possible ways of selecting ‘K’ cities.

Approaches (1)
Brute force

This problem is an NP-Hard problem i.e there exists no polynomial-time solution for it. So we cannot do anything more than brute force for the exact solution. 

 

Algorithm

  • This is a recursive algorithm.
  • Create an empty integer list/vector ‘SELECTED’ of size ‘N’.
  • Initialize an integer variable ‘RESULT’:= INF.
  • We make a recursive function, let it be kCenterHelper(K, N, SELECTED, DIST). It will one by one generate all possible ways of selecting ‘K’ cites from ‘N’.
    • If K = 0, then do the following -: 
      • Initialize an integer variable ‘MAXDIST’: = 0.
      • Run a loop where ‘i’ ranges from 0 to ‘N’-1. For each ‘i’ iterate over ‘SELECTED’ and find the minimum distance of the ith city from any of the selected cities and update ‘MAXDIST’ with the maximum of its current value and this minimum distance.
      • Do ‘RESULT’:= max(‘RESULT’, ‘MAXDIST’).
    • Otherwise, let ‘PREV’ be -1 if ‘SELECTED’ is empty, else it should be the last integer of ‘SELECTED’, Run a loop where ‘i’ ranges from ‘PREV’+1 to ‘N’ -1 and for each ‘i’ do the following -:
      • Append ‘i’ in ‘SELECTED’.
      • Call kCenterHelper(K-1, N, SELECTED, DIST).
      • Pop last element from ‘SELECTED’.
  • Call kCenterHelper with given values, and return ‘RESULT’.
Time Complexity

O(N * K * (2 ^ N)), where ‘N’ and ‘K’ respectively represent the number of cities in Ninja Land and the number of cities where the server needs to be installed.

 

The number of ways of selecting ‘K’ cities out of ‘N’ cannot exceed 2 ^ N. And it will take us O(N * K) time to find the maximum distance for each combination of selected cities. Thus its time complexity should be order O(N * K * (2 ^ N)).

Space Complexity

O(K), where  ‘K’ represents the number of cities where the server needs to be installed.

 

The extra space used by the recursion stack and array/list ‘SELECTED’ both are O(K). Thus overall space complexity will be O(K) + O(K) = O(K).

Code Solution
(100% EXP penalty)
K Centers
Full screen
Console