Problem
Submissions
Hints & solutions
Discuss
Knight Dialer
Moderate
0/80
Problem statement
You are given a number pad as shown in the figure below, and you also have a ‘knight’ piece from chess. Your task is to determine how many different ‘N’ digit numbers can be formed by placing the ‘knight’ anywhere on the number pad and moving the ‘knight’ according to the rules of chess.
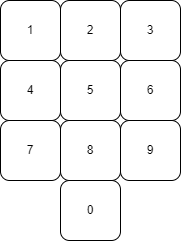
Return the solution modulo 10^9 + 7.
You are given ‘N’ = 2, all the unique 2 digit numbers formed moving the knight on the number pad are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]. Hence the answer is 20.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line of input contains a single integer ‘T’ representing the number of test cases.
The first and the only line of each test case contains a single integer ‘N’.
Print a single integer for each test case, representing the number of distinct numbers formed by moving the knight.
Print a separate line for each test case.
Constraints
1 <= T <= 10
1 <= N <= 10^3
Time Limit: 1 sec
You do not need to print anything. It has already been taken care of. Just implement the given function.
Sample Input 1:
2
2
1
Sample Output 1:
20
10
Explanation:
For the first test case, ‘N’ = 2, all the unique 2 digit numbers formed moving the knight on the number pad are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]. Hence the answer is 20.
For the second test case, ‘N’ = 1, all the unique 1 digit numbers formed moving the knight on the number pad are [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]. Hence the answer is 10.
Sample Input 2:
2
1232
99
Sample Output 2:
506096595
168850940
Hint
Hint 1
Hint 2
Hint 3
Try the brute force approach recursively.
Approaches (3)
Approach 1
Approach 2
Approach 3
Recursive Brute Force
In this approach, we will visit each position in the number pad and count the number of distinct numbers that can be dialled. We will make a map of all the places to be visited from a given number.
We create a recursive function helper(currPos, nextPositions, digitsRem), currPos is the current key on the number pad, nextPositions is the map of the next positions from any key, and digitsRem is the number of digits left to form the number.
Algorithm:
- In the helper(currPos, nextPositions, digitsRem),
- If digitRem is equal to 1, return 1
- Set ans as 0
- Iterate nextPos through nextPositions[currentPos]
- Add helper(nextPos, nextPositions, digitsRem - 1) to ans.
- Return ans modulo 10^9 + 7
- In given function
- If n is equal to 1, return 10
- Set ans as 0
- Create a map nextPositions with integer key and a list as value, corresponding to the next position of the knight from the key.
- Iterate i from 0 to 9
- Add helper(i, nextPositions, n) to ans.
- Return ans modulo 10^9 + 7
Time Complexity
O(2^N), Where N is the given integer.
For each call, we are recursively calling the function again on an average of 2 times . Hence the time complexity is O(2^N).
Space Complexity
O(N), Where N is the given integer.
The recursion stack will take O(N) space.
Code Solution
(100% EXP penalty)
Knight Dialer
C++ (g++ 5.4)
Console




