Problem
Submissions
Hints & solutions
Discuss
Day 7 : Langford Pairing
Easy
0/40
Average time to solve is 10m
13 upvotes
Asked in companies


Problem statement
You are given a positive integer N. Return a list of integers of size 2N containing all the integers from 1 to N (both inclusive) twice arranged according to Langford pairing. If no such pairing exists return -1 is the only list element.
Note:There may be more than one Langford pair possible, you need to return anyone permutation.
For N = 4, one possible Langford pairing will be:-
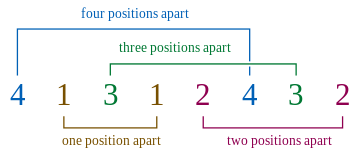
Detailed explanation ( Input/output format, Notes, Images )
Input format:
The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then, the T test cases follow.
The first and only line of each test case or query contains the integer N.
The only line of output contains “Valid” if the answer is correct and “Invalid” if it’s not, without quotes.
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 5
0 <= N <= 32
Time Limit: 1 sec
Sample Input 1:
2
4
5
Sample Output 1:
4 1 3 1 2 4 3 2
-1
Explanation For Sample Input 1:
For the first test case:
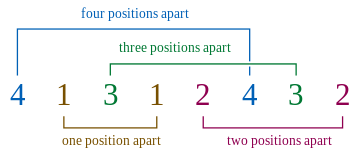
For the second test case:
No Langford pairing is possible, hence print -1.
Sample Input 2:
1
15
Sample Output 2:
15 13 14 8 5 12 7 11 4 10 5 9 8 4 7 13 15 14 12 11 10 9 6 3 1 2 1 3 2 6
Hint
Hint 1
First off, observe that the question is basically a permutation question, the only twist is that once we fix the first position of one element, the other position of that element is fixed itself.
Approaches (1)
Approach 1
Recursion
It can be observed with some examples that for any number N, the permutation following Langford pairing is possible only if either N mod 4 is 0 or 3. Thus, Langford pairing is possible for 3, 4, 7, 8, etc, and not possible for 1, 2, 5, 6, etc. Now to find the sequence,
- If N mod 4 is 1 or 2, return -1.
- Otherwise, we will use recursion to generate the sequence.
- Create an array of size 2*N and initialize all its elements with 0.
- Now, we will fill the elements in the array keeping in mind the following things:
- We will start filling the array from the maximum number i.e N.
- Once we fill an integer A at the position i, we will also fill integer A at position i+A+1.
- Thus we will call langfordPairing(result, N) to find the sequence where the result is the list in which we will save one required permutation
Algorithm:
bool langfordPairing(result, N):
- If N is 0, there is no element left to put in the sequence, return true.
- For i = 0 to result.size() - N - 1:
- If (i)th and (i+N+1)th position i.e the first and second possible positions for placing N are vacant and also within range of the array result.
- Then add N to the sequence, arr[i] = N, arr[i + N + 1] = N.
- Recursively fill the rest of the elements and find whether it is possible to make the sequence or not, isExists = langfordPairing(arr, N-1, result).
- If isExists is true, then we have found the sequence. Thus return true.
- Otherwise, we need to remove N from the slots, arr[i] = 0, arr[i + N + 1] = 0.
- If (i)th and (i+N+1)th position i.e the first and second possible positions for placing N are vacant and also within range of the array result.
- No such sequence exists, return false.
Time Complexity
O(N^N) per test case, where N is the input integer.
In the worst case, we are calling a loop of 2*N size for N numbers.
It should be noted that complexity will actually be less than N^N as, if the answer is possible, we will find it in the halfway itself and if the answer isn’t possible, we will return the function in constant time.
Space Complexity
O(N) where N is the size of the array.
In the worst case, extra space is used by the recursion stack.
Code Solution
(100% EXP penalty)
Day 7 : Langford Pairing
Javascript (node v10.20.0)
Console
