Problem

Submissions

Hints & solutions

Discuss

M-Coloring Problem

Moderate

0/80

Average time to solve is 15m

Contributed by

89 upvotes

Asked in companies

Problem statement

You are given an undirected graph as an adjacency matrix consisting of 'v' vertices and an integer 'm'.

You need to return 'YES' if you can color the graph using at most 'm' colors so that no two adjacent vertices are the same. Else, return 'NO'.

For example:

Input:
If the given adjacency matrix is:
[0 1 0]
[1 0 1]
[0 1 0] and 'm' = 3.

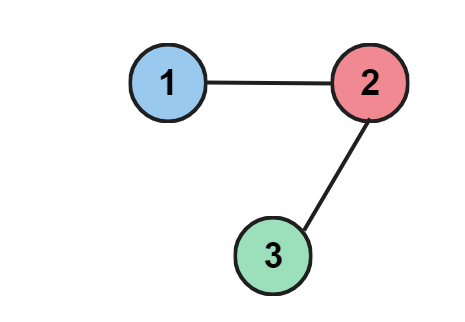
Output: YES

Explanation:
The given adjacency matrix tells us that 1 is connected to 2 and 2 is connected to 3. We can use three different colors and color all three nodes.
Hence we return true.

Detailed explanation ( Input/output format, Notes, Images )

Input Format:

The first line contains two space-separated integers, 'v' and 'm', denoting the number of vertices in the undirected graph and the number of colors, respectively.

Each of the next 'v' lines contains 'v' integers denoting the adjacency matrix of the undirected graph.

Output Format:

You need to return “YES” if we can color the graph with at most M colors. Otherwise, return “NO”. (without the inverted commas)

Note:

You are not required to print the expected output. It has already been taken care of. Just implement the function.

Sample Input 1:

Sample Output 1:

YES

Explanation of Input 1:

The adjacency matrix tells us that 1 is connected to 2, and 2 is connected to 3. We can see that a minimum of 2 colors would be needed to color the graph. So it is possible to color the graph in this case.

Sample Input 2:

Sample Output 2

NO

Constraints:

1 ≤ v ≤ 20
1 ≤ m ≤ v

Time Limit: 1 sec

Hint 1

Hint 2

Take all different color combinations possible

Approaches (2)

Approach 1

Approach 2

Brute Force

We generate all possible combinations of colors possible for coloring the given graph.
This can be done recursively by assigning a node each color from 1 to M and doing the same for all nodes.
We further check if the adjacent vertices don’t have the same color.
If we find such a combination of vertices, we return “YES”. Otherwise, we return “NO”.

Time Complexity

O(M ^ V + M * V * V) where V is the number of vertices in the graph and M is the maximum number of colors allowed.

This is because, for each node, there are M possibilities to color it and there are V nodes, which gives us M *...* M (V times) = M ^ V. Additionally, we iterate the adjacency matrix for each of the M colors which adds an extra complexity of M * V * V, which leads to total time complexity of O(M ^ V + M * V * V).

Space Complexity

O(V) where V is the number of vertices in the graph.

Because we make an array of size V for storing the colors of each vertex.

(75% EXP penalty)

(100% EXP penalty)

M-Coloring Problem

Console