Matrix Multiplication

Moderate
0/80
Average time to solve is 15m
profile
Contributed by
11 upvotes
Asked in companies
UberAppleMicrosoft

Problem statement

Ninja has been given two sparse matrices ‘MAT1’ and ‘MAT2’ of integers having size ‘N’ x ‘M’ and ‘M’ x ‘P’, respectively.

A sparse matrix is a matrix that contains very few non-zero elements.

Ninja has to find the matrix formed by the multiplication of ‘MAT1’ and ‘MAT2’. As Ninja is busy with some other tasks so he needs your help. Can you help Ninja to find the matrix formed by the multiplication of ‘MAT1’ and ‘MAT2’?

Note: The number of columns in ‘MAT1’ i.e ‘M’ is equal to the number of rows in ‘MAT2’ i.e ‘M’. It means we can always multiply ‘MAT1’ with ‘MAT2’.

For example:

For the ‘MAT1’ and ‘MAT2’ given below, ‘MAT3’ is the matrix formed by multiplying ‘MAT1’ and ‘MAT2’.

img

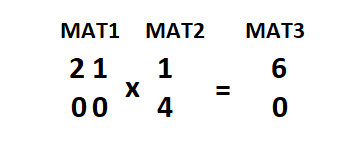
1. MAT3[0][0] = MAT1[0][0] * MAT2[0][0] + MAT1[0][1] * MAT2[1][0]  ie. 2 * 1 + 1 * 4 = 6
2. MAT3[1][0] = MAT1[1][0] * MAT2[1][0] + MAT1[1][1] * MAT2[1][0] ie. 0 * 6 + 0 * 4 = 0
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains an integer ‘T’ denoting the number of test cases. Then each test case follows.

The first line of each test case contains four space-separated integers ‘N’, ‘M’, ‘M’, ‘P’ where ‘N’ and ‘M’ representing the number of rows and columns of ‘MAT1’ respectively and ‘M’ and ‘P’ representing the number of rows and columns of ‘MAT2’ respectively. 

The next ‘N’ lines of each test case contain ‘M’ single space-separated integers denoting the values of ‘MAT1’. Then the next ‘M’ lines contain ‘P’ single space-separated integers denoting the values of ‘MAT2’
Output Format : 
For each test case, return the matrix ‘MAT3’ which will be formed by multiplying ‘MAT1’ and ‘MAT2’.
Note: 
You are not required to print the expected output; it has already been taken care of. Just implement the function.
Constraints: 
1 <= ‘T’ <= 100
1 <= ‘N’, ‘M’ and ‘P’ <= 100
-10^5 <= ‘MAT1[i][j]’ and ‘MAT2[i][j]’ <= 10^5

Time limit: 1 sec
Sample Input 1:
1
2 1 1 2
2
0
1 2
Sample Output 1:
2 4
0 0

Explanation for Sample Output 1:

For sample test case 1: 
1. MAT3[0][0] = MAT1[0][0] * MAT2[0][0] ie. 2 * 1 = 2
2. MAT3[0][1] = MAT1[0][0] * MAT2[0][1] ie. 2 * 2 = 4
3. MAT3[1][0] = MAT1[0][1] * MAT2[0][0] ie. 0 * 1 = 0 
4. MAT3[1][1] = MAT1[1][1] * MAT2[0][1] ie. 0 * 2 = 0
Sample Input 2:
2
1 1 1 2
3
1 0
1 1 1 1
-1
7
Sample Output 2:
3 0
-7

Explanation for Sample Output 1:

For sample test case 1: 
1. MAT3[0][0] = MAT1[0][0] * MAT2[0][0] ie. 3 * 1 = 3
2. MAT3[0][1] = MAT1[0][0] * MAT2[0][1] ie. 3 * 0 = 0

For sample test case 2: 
1. MAT3[0][0] = MAT1[0][0] * MAT2[0][0] ie. -1 * 7 = -7
Hint

Think of the Brute Force Approach.

Approaches (2)
Brute Force
  • We can get the matrix ‘MAT3’ using 3 nested loops.
  • To get the (‘i’, ‘j’) cell element of the matrix ‘MAT3’, we need to multiply each element of the ‘i’th row of ‘MAT1’ with the ‘j’’th column of the matrix ‘MAT2’ and finally add all the results.

 

Here is the complete algorithm: 

  • Make a 2D array/list ‘MAT3’ having ‘N’ rows and ‘P’ columns.
  • Run a for loop from ‘i’ = 0 to ‘i’ < ‘N’ and for each ‘i’ do the following:
    • Run a for loop from ‘j’ = 0 to ‘j’ < ‘P’ and for each ‘j’ do the following:
      • Make a variable ‘sum’ = 0.
      • Run a for loop from ‘k’ = 0 to ‘k’ < ‘M’ and for each ‘k’ do the following:
        • ‘sum’ = ‘sum’ + ‘MAT1[i][k]’ * ‘MAT2[k][j]’.
      • Update ‘MAT3[i][j]’ = ‘sum’.
  • Return ‘MAT3’.

  

Time Complexity

O(N * M * P), where ‘N’ and ‘M’ denote the number of rows and columns of the matrix ‘MAT1’ and ‘P’ denotes the number of columns in ‘MAT2’.

 

We are using 3 nested loops. Hence, the overall time complexity is O(N * M * P).

Space Complexity

O(1).

 

Because we are not using any extra space for finding our resultant answer.

Code Solution
(100% EXP penalty)
Matrix Multiplication
Full screen
Console