Maximize the sum

Moderate
0/80
Average time to solve is 15m
profile
Contributed by
16 upvotes
Asked in companies
IntuitAmazonThought Works

Problem statement

You are given two sorted arrays of distinct integers, ‘ARR1’ and ‘ARR2’. If you find a common element in both arrays, you can switch from one array to another.

Your task is to find a path through the intersections i.e common integers of ‘ARR1’ and ‘ARR2’, that produces maximum sum and return that maximum sum as the answer.

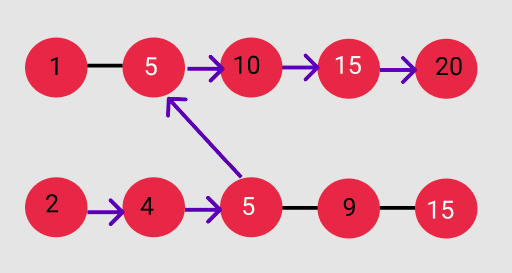
For example: 
Let ‘ARR1’ = [1, 5, 10, 15, 20]  and ‘ARR2’ = [2, 4, 5, 9, 15]
In this example, common points are 5, 15.

First, we start with ARR2 and take the sum till 5 (i.e. sum = 11). Then we will switch to ‘ARR1’ at element 10 and take the sum till 15. So sum = 36. Now no element is left in ‘ARR2’ after 15, so we will continue in array 1. Hence sum is 56. And the path is 2 -> 4 -> 5 -> 10 -> 15 -> 20.

array

Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.

The first line of each test case contains two space-separated integers, ‘N’ and ‘M,’ representing the number of elements in ‘ARR1’ and ‘ARR2’.

The second line of each test case contains ‘N’ single space-separated integers denoting the values of ‘ARR1’.

The third line of each test case contains ‘M’ single space-separated integers denoting the values of ‘ARR2’.
Output Format : 
For each test case, print the maximum sum value.

Print the output of each test case in a separate line.
Note: 
You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints: 
1 <= ‘T’ <= 100
1 <= ‘N’, ’M’ <= 10^4
1 <= ‘ARR1[i]’, ‘ARR2[j]’ <= 10^5

Time Limit: 1 second
Sample Input 1 :
2
5 4
1 2 4 5 6
2 3 4 7 
5 5
1 2 3 4 5
1 2 3 4 5
Sample Output 1:
21
15
Explanation For Sample Output 1:
For sample test case 1: 
Common points are: 2, 4

First, we start with ‘ARR1’ and take the sum till 2 (i.e. sum = 3). Then we will switch to ‘ARR2’ at element 2 and take the sum till 4 (i.e. sum = 10). Then we will switch to ‘ARR1’ at element 4 and take the sum till the end of the ‘ARR1’. Hence sum is 21.

The path is 1 -> 2 -> 3 -> 4 -> 5 -> 6.

For sample test case 2: 
Common points are : 1, 2, 3, 4, 5

First, we start with ARR1 and take the sum till 1 (i.e. sum = 1). Then we again continue with ‘ARR1’  and take the sum till 2 (i.e., 3). Similarly, we continue with 'ARR1' and keep on adding elements until the last element. Hence sum is 15.

And the path is 1 -> 2 -> 3 -> 4 -> 5.
Sample Input 2 :
2
5 4
2 4 5 8 10
4 6 8 9
4 4
1 2 3 4
5 6 7 8
Sample Output 2:
30
26
Hint

Think of a Recursive solution.

Approaches (3)
Recursive

In this problem, our primary focus is on the common elements i.e. an element that is present in both the arrays. Then, we have to decide whether we have to make a switch. So for that, first we store all the elements of ‘ARR1’ and ‘ARR2’ into ‘MAP1’ and ‘MAP2’ respectively. 

 

Now we call our ‘maximiseSumHelper’ function. We call this function for both cases i.e starting with ‘ARR1’ and starting with ‘ARR2’. Then we return the maximum of the two cases. During the recursive call, if we find a common element that is present in both the arrays, then we have two options at that point i.e. either we can switch to the other array or ontinue with the same array.

 

Here is the algorithm :

 

  • We declare two HashMaps i.e. ‘MAP1’ and ‘MAP2’ in which we store elements of ‘ARR1’ and ‘ARR2’ respectively.
  • Return max(maximiseSumHelper(‘ARR1’, ‘ARR2’, 1, 0),maximiseSumHelper(‘ARR1’, ‘ARR2’, 2, 0))

 

maximiseSumHelper(‘ARR1’, ‘ARR2’, ‘currArr’, ‘currInd’) function works as follows:

 

  • Base Case:
    • If the ‘currInd’ is greater than or equal to the current array's size, we have reached the end of the array. So we return 0. 
  • We declare a variable ‘maximumSum’ in which we store our answer.
  • If ‘currArr’ == 1:
    • ‘maximumSum’ = ‘ARR1[‘currInd’]’ + maximiseSumHelper(‘ARR1’, ‘ARR2’, ‘currArr’, ‘currInd’ + 1)
    • If ‘ARR1[currInd]’ is present in both the arrays:
      • Now we take both the cases i.e. we can either switch from the current array to the other array or we will continue with the same array.
  • Else
    • ‘maximumSum’ = ‘ARR2[‘currInd’]’ + ‘maximiseSumHelper(‘ARR1’, ‘ARR2’, ‘currArr’, ‘currInd’ + 1)
    • If ‘ARR2[currInd]’ is present in both the arrays:
      • Again, we take both cases i.e. we can switch from the current array to the other array or we will continue with the same array.
  • Finally, return ‘maximumSum’.
Time Complexity

O(2 ^ max(N, M))  where ‘N’ and ‘M’ denote the number of elements in ‘ARR1’ and ‘ARR2’, respectively.

 

Because in the worst case we have at most 2 recursive calls at every index.

 

Let’s take an example:

If both the arrays contain the same values, let ‘ARR1’ = [1, 2, 3, 4] and ‘ARR2’ = [1, 2, 3, 4]. So, in this case, at every index, we have two choices i.e either we can switch to the other array or we can continue with the same array.

Space Complexity

O(max(N, M))  where 'N’ and ‘M’ denote the number of elements in ‘ARR1’ and ‘ARR2’, respectively.

 

Because we use hashMaps to store all the elements of ‘ARR1’ and ‘ARR2’. And the recursion stack also goes up to max(N, M).

Let’s take an example: Let ‘ARR1’ = [1, 2, 3] and ‘ARR2’ = [4, 5, 6]. In this example, there is no common point so our recursive function first goes to all the elements of ‘ARR1’, returns an answer, and then it goes to all the elements.

Code Solution
(100% EXP penalty)
Maximize the sum
Full screen
Console