Problem
Submissions
Hints & solutions
Discuss
Maximum Equal Stack Sum
Easy
0/40
Average time to solve is 15m
25 upvotes
Asked in companies


Problem statement
Given three filled stacks namely ‘stack1’ ‘stack2’ and ‘stack3’ of positive numbers, the task is to find the possible equal maximum sum of the stacks with the removal of top elements allowed.
For example, let the stacks be:
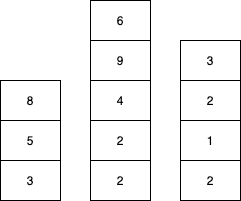
We can see that currently,
the sum of stack 1 is: 8+5+3 = 16
the sum of stack 2 is: 2+2+4+9+6 = 23
the sum of stack 3 is: 2+1+2+3 = 8
So they are not equal.
However, if we pop {8} from stack 1, {6,9} from stack 2 and nothing from stack 3,
We get the sum as :
Stack 1: 16-8=8
Stack 2: 23-15=8
Stack 3: 8-0=8
We can see that now the sum of all three stacks are equal which is 8 and it is the highest possible, hence we return 8.
Note:1. Do not print anything, just return an integer which is the maximum possible sum for the three stacks.
2.It is guaranteed that the elements in the stack are positive integers.
3.It can be proved that a non-negative integer answer always exists.
Detailed explanation ( Input/output format, Notes, Images )
Input format:
The first line of input contains an integer ‘T’ denoting the number of test cases.
The next ‘3*T’ lines represent the ‘T’ test cases.
The first line of each test case contains a stream of integers which are in the order of which the elements are pushed in ‘stack1’. The stream ends when the input is -1. The top of the stack is the element just before -1. Note that -1 is not pushed in the stack.
The second line of each test case contains a stream of integers which are in the order of which the elements are pushed in ‘stack2’. The stream ends when the input is -1. The top of the stack is the element just before -1. Note that -1 is not pushed in the stack.
The third line of each test case contains a stream of integers which are in the order of which the elements are pushed in ‘stack3’. The stream ends when the input is -1. The top of the stack is the element just before -1. Note that -1 is not pushed in the stack.
For each test case, return a single integer denoting the maximum equal sum for the three stacks.
Constraints:
1 <= T <= 50
1<= N <=10^4
1<= stackData <=10^9
Where ‘T’ is the total number of test cases, ‘N’ denotes the number of elements in any of the stacks and ‘stackData’ represents the data in the stacks.
Time limit: 1 second
2
2 4 1 9 -1
1 6 3 -1
5 2 1 -1
8 2 1 -1
1 1 1 -1
6 3 -1
7
0
Test Case 1:
The stacks are:

We can see that currently,
the sum of stack 1 is:9+1+4+2=16
the sum of stack 2 is: 3+6+1=10
the sum of stack 3 is: 5+2+1=8
So they are not equal.
However, if we pop {9,1} from stack 1 {3} from stack 2 and {1} from stack 3,
We get the sum as :
Stack 1: 16-9-1=7
Stack 2: 10-3=7
Stack 3: 8-1=7
We can see that now the sum of all 3 stacks are equal which is 7 and it is the highest possible, hence we return 7.
Test Case 2:
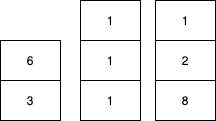
We can see that currently,
the sum of stack 1 is: 6+3=9
the sum of stack 2 is: 1+1+1=3
the sum of stack 3 is: 1+2+8=11
So they are not equal.
Now, no matter what we do we can never make the sum equal to any number for all the three stacks except 0. So, in this case, we return 0.
2
2 2 4 6 -1
14 6 8 1 -1
7 7 6 4 -1
9 9 9 9 -1
20 7 -1
5 6 7 9 -1
14
27
Hint
Hint 1
Hint 2
Hint 3
Just find all possible sums for all the stacks.
Approaches (3)
Approach 1
Approach 2
Approach 3
Brute Force
Approach:
- The key idea is to find all possible sums for each of the stacks and checking if there is any number which is equal to the sum of all three stacks.
- We can find all possible sums by first finding the initial sum of the three stacks and popping elements one by one and then storing the sums in an array.
- We do the same for all three stacks.
- Then we check if any number is found in all three arrays. If yes, we return the maximum number.
- Else we will always have an answer as 0 as we can just empty all three stacks and their sum will be the same.
Keeping the above example in mind, we can write the following Recursive solution:
- First, we define a function ‘findStackSum’ which just finds the sum of all elements in the stack by simply popping the elements and storing them in a variable called ‘sum’.
- We define three variables ‘stk1Sum’, ‘stk2Sum’, and ‘stk3Sum’ which stores the sum of all three stacks.
- Then we make three arrays ‘stk1AllSums’ ‘stk2AllSums’ and ‘stk3AllSums’ which store all possible sums for the three stacks.
- We do this by popping from the stack and storing the difference of ‘stkSum’ and the current top in the array and then updating the ‘stkSum’
- Then we use three nested loops to iterate through these three arrays to find the number which is present in all three stacks. Since the arrays are in descending order, the first time we find such sum is guaranteed to be the maximum. Find the sum and return it.
- If no such sum is found, just return 0 as it is always an answer.
Time Complexity
O(n^3), Where ‘n’ denotes the maximum number of elements of the three stacks.
Since we need three nested loops to search if there is a max element, the complexity is order of n^3.
Space Complexity
O(n), Where ‘n’ denotes the maximum number of elements of the three stacks.
we need space to store three arrays with all possible sums.
Code Solution
(100% EXP penalty)
Maximum Equal Stack Sum
Javascript (node v10.20.0)
Console
