Maximum Path Sum in the matrix

Moderate
0/80
Average time to solve is 35m
profile
Contributed by
260 upvotes
Asked in companies
AmazonPayPalMicrosoft

Problem statement

You have been given an N*M matrix filled with integer numbers, find the maximum sum that can be obtained from a path starting from any cell in the first row to any cell in the last row.

From a cell in a row, you can move to another cell directly below that row, or diagonally below left or right. So from a particular cell (row, col), we can move in three directions i.e.

Down: (row+1,col)
Down left diagonal: (row+1,col-1)
Down right diagonal: (row+1, col+1)
Detailed explanation ( Input/output format, Notes, Images )
Input format : 
The first line contains an integer 'T', which denotes the number of test cases or queries to be run. Then the test cases follow.

The first line of each test case contains two Integers 'N' and 'M' where 'N' denotes the number of rows in the given matrix. And 'M' denotes the number of columns in the given matrix.

The next 'N' line of each test case contains 'M' space-separated integers denoting the cell elements.
Output format : 
For each test case/query, print the maximum sum that can be obtained by taking a path as described above.

Output for every test case will be printed in a separate line.
Note : 
You do not need to print anything. It has already been taken care of.
Constraints : 
1 <= T <= 50
1 <= N <= 100
1 <= M <= 100
-10^4 <= matrix[i][j] <= 10^4

Where 'T' is the number of test cases.
Where 'N' is the number of rows in the given matrix, and 'M' is the number of columns in the given matrix.
And, matrix[i][j] denotes the value at (i,j) cell in the matrix.

Time Limit: 1sec
Input 1 :
2
4 4
1 2 10 4
100 3 2 1
1 1 20 2
1 2 2 1
3 3
10 2 3
3 7 2
8 1 5
Output 1 :
105
25
Explanation Of Input 1 :
In the first test case for the given matrix,

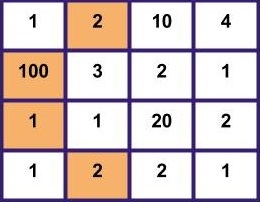
Example

The maximum path sum will be 2->100->1->2, So the sum is 105(2+100+1+2).

In the second test case for the given matrix, the maximum path sum will be 10->7->8, So the sum is 25(10+7+8).
Input 2 :
2
3 3
1 2 3
9 8 7
4 5 6
4 6
10 10 2 -13 20 4
1 -9 -81 30 2 5
0 10 4 -79 2 -10
1 -5 2 20 -11 4
Output 2 :
17
74
Explanation Of Input 2 :
In the first test case for the given matrix, the maximum path sum will be 3->8->6, So the sum is 17(3+8+6).

In the second test case for the given matrix, the maximum path sum will be 20->30->4->20, So the sum is 74(20+30+4+20).
Hint

Does it make sense to explore all the possible paths?

Approaches (3)
Brute Force

The basic approach is that we are going to explore all possible paths recursively from the first row for each cell and return the maximum sum among all paths. Steps are as follows:

  1. Start exploring the path from each cell of the first row.
  2. And the path can end at any cell of the last row.
  3. If any move gets out of the boundary of the given matrix, then we return negative infinity, i.e. INT_MIN, because we do not want to consider that move in our path.
  4. Now we can move to follow three cells from the cell (row, col)
    • Down move : (row+1, col)
    • Down left diagonal : (row+1, col-1)
    • Down right diagonal : (row+1, col+1)
  5. Now among the above three paths, which path has the maximum sum that will be the maximum path sum from (row, col) to any cell of the last node. So return the sum of the current cell and maximum path what we got from above three paths.
  6. So above steps can be recursively defined as:
getMaxPathSum(row,col)=matrix[row][col]+max(getMaxPathSum(row+1,col),*max(getMaxPathSum(row+1,col+1),getMaxPathSum(row+1,col-1))
Time Complexity

O(M*3^(N*M)), Where ‘N’ is the number of rows and ‘M’ is the number of columns in the given matrix.
 

We are exploring all possible paths for all cells from the first row. So there are ‘M’ cells in the first row, and each cell is going to explore all possible paths. So for each cell in the matrix, we have three choices to move, so there are N*M cells, and each cell has three moves, i.e. down, down left diagonal and downright diagonal. So for N*M cell, we will have 3^(N*M) moves. So overall complexity will be O(M*3^(N*M)).

Space Complexity

O(N), Where ‘N’ is the number of rows in the given matrix.
 

We are using recursion to explore the path so for each step, we are pushing the function into the stack, and there can be total ‘N’ steps Because for each step we are going one step down. So overall space complexity is O(N).

Code Solution
(100% EXP penalty)
Maximum Path Sum in the matrix
Full screen
Console