Maximum Sum BST

Hard
0/120
Average time to solve is 50m
profile
Contributed by
18 upvotes
Asked in companies
AmazonOLX GroupExpedia Group

Problem statement

You are given a Binary Tree ‘root’. The given Binary Tree may or may not be a Binary Search Tree(BST) itself. Your task is to find the maximum sum of node values of any subtree that is a Binary Search Tree(BST).

Binary Search Tree is defined as follows: 
1) If the left subtree exists it should contain only nodes with values less than the current node's value.

2) If the right subtree exists it should contain only nodes with values greater than the current node's value.

3) Both the left and right subtrees should also be Binary Search Tree.
Example : 

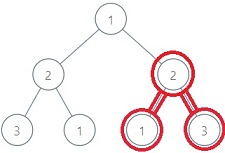
For the above binary tree, the BST with the maximum possible sum is marked with RED colour, the sum of this BST is equal to 6.

 

Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains a single integer ‘T’ denoting the number of test cases, then each test case follows

The first line of each test case contains the elements of the tree in the level order form separated by a single space.

If any node does not have a left or right child, take -1 in its place. 

For example, the input for the tree depicted in the below image would be :

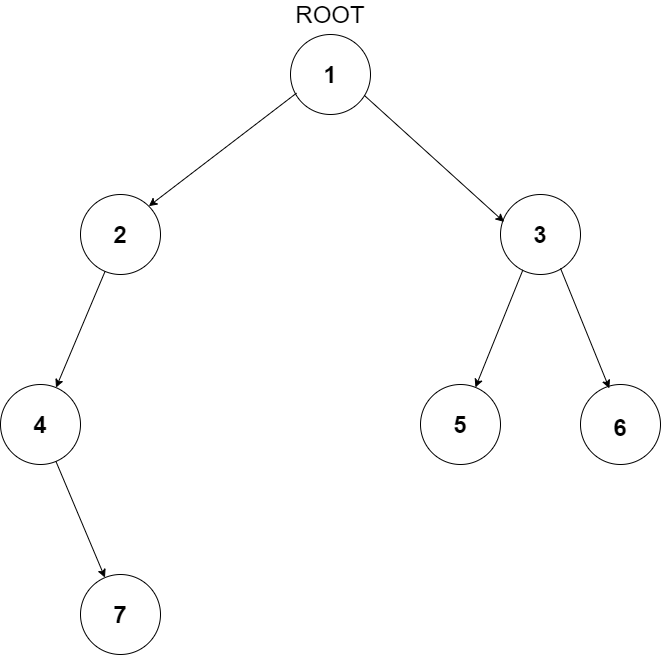
Example

1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null (-1).
Output Format : 
For each test case print the maximum sum possible.

Output for each test case will be printed in a separate line.
Note : 
You are not required to print anything; it has already been taken care of. Just implement the function.
Constraints : 
1 <= T <= 10      
1 <= Number Of Nodes <= 5*10^4
0 <= Node.data <= 10^5

Time limit: 1 sec
Sample Input 1 : 
2
4 2 6 1 3 5 7 -1 -1 -1 -1 -1 -1 -1 -1
1 2 3 -1 -1 -1 -1
Sample Output 1 : 
28
3
Explanation Of Sample Output 1 : 

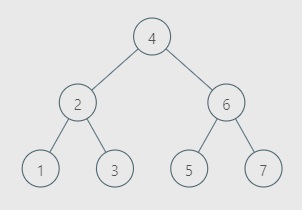
For test case 1, the image above shows the input tree:
Given binary tree is itself a BST, also as all the nodes have positive values hence entire tree will be the subtree with maximum sum. Sum of all the node values is: 1 + 2 + 3 + 4 +5 + 6 + 7 = 28 


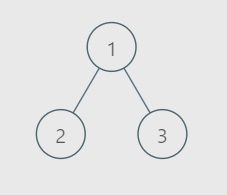
For test case 2, the image above shows the input tree:
The subtree with a single node and node value equal to 3 is the BST with maximum sum.
Sample Input 2 : 
2
2 1 3 -1 -1 -1 -1
1 3 2 2 4 1 3 -1 -1 -1 -1 -1 -1 -1 -1
Sample Output 2 : 
6
9
Hint

Traverse the entire tree and for each node evaluate sum of the subtree if it is a BST.

Approaches (2)
Recursion

 

Traverse the tree using recursion. For each node first check if it is a BST, if it is a BST then calculate the sum of node values of the subtree rooted at the current node. Use variable ans to store the maximum BST sum calculated till now, and finally return the value of ans.

 

The steps are as follows :

  1. Initialize ans equal to 0.
  2. Create a recursive function traverseTree which takes the following parameters: curNode to point the current node and ans to store the maximum possible sum.
  3. The initial call is made with the given root node.
  4. In traverseTree for each node check if subtree rooted at current node is a BST.
  5. If found a BST, calculate sum of the subtree rooted at the current node.
  6. Check if sum is greater than current value of ans, if so set ans equal to sum.
  7. Check if the left/right child exists, and recursively calculate same things for them.
  8. Return the value of ans.
Time Complexity

O( N^2 ), where N is the number of nodes in the binary tree.


Through recursion, for each node we evaluate it’s subtree which can itself have ~N nodes. Hence the time complexity is O(N^2).

Space Complexity

O( N ), where N is the number of nodes in the binary tree.


If the given binary tree is in form of a straight-chain(bamboo) then at max N recursive calls will be present in the stack frame. Hence the space complexity is O(N).

Code Solution
(100% EXP penalty)
Maximum Sum BST
Full screen
Console