Maximum Sum Of Nodes

Moderate
0/80
Average time to solve is 30m
profile
Contributed by
38 upvotes
Asked in companies
AmazonGoldman SachsDunzo

Problem statement

You have been given a binary tree with an integer value associated to each node. You are supposed to choose a subset of these nodes such that the sum of these chosen nodes is maximum. Keep in mind that no two of the chosen nodes must be adjacent to each other.

Note : 
Two nodes are said to be adjacent to each other if they are directly connected to each other. This means that if a node is taken as part of the sum, then none of its children can be considered for the same and vice versa.
For example : 
For the given binary tree

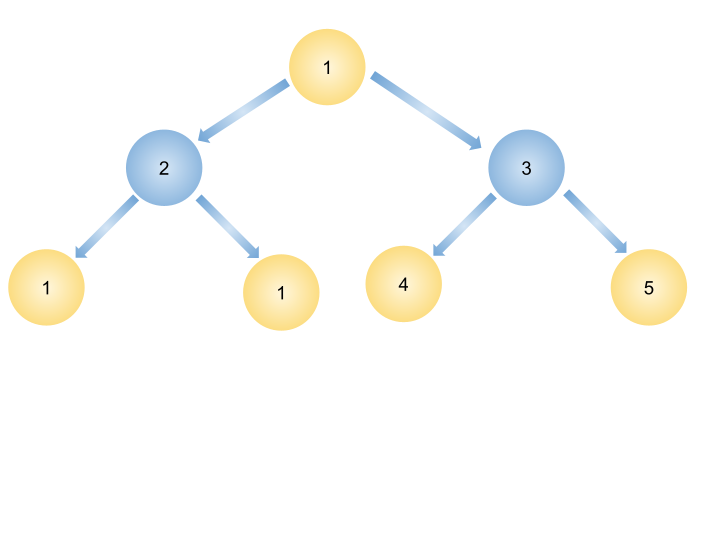
Example

Nodes used in consideration for maximum sum such that no two of them are adjacent are highlighted. Maximum sum of nodes = 1 + 1 + 1 + 4 + 5 = 12.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases are as follows.

The first line of each test case contains elements of the tree in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image would be :

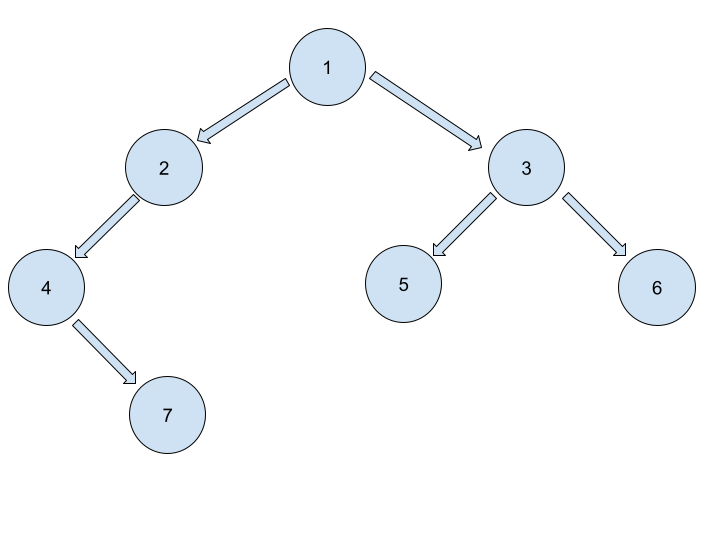
Example

Input Format :   
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation : 
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null(-1).
Note : 
The above format was just to provide clarity on how the input is formed for a given tree. 
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format : 
For each test case, print the maximum sum of nodes keeping the above constraints in mind.

Print the output of each test case in a separate line.
Note : 
You do not need to print anything; it has already been taken care of. You just need to return the maximum sum of nodes.
Constraints : 
1 <= T <= 100
0 <= N <= 3000
1 <= data <= 10^4

 Where ‘T’ is the number of test cases, and ‘N’ is the total number of nodes in the binary tree, and “data” is the value of the binary tree node.

Time Limit : 1 sec
Sample Input 1 :
1
1 2 3 1 -1 4 5 -1 -1 -1 -1 -1 -1
Sample Output 1 :
11
Explanation of Sample Input 1 :
The binary tree will look like this:

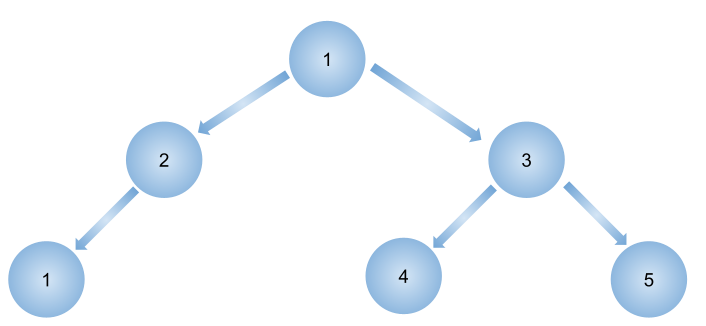
Example

Example

In the above Binary tree chosen nodes(highlighted) such that the sum of nodes is maximum and they are not adjacent to each other = 2, 4, 5 and their sum = 2 + 4 + 5 = 11. Hence, the output is 11
Sample Input 2 :
2
1 2 3 -1 -1 -1 -1
7 -1 -1
Sample Output 2 :
5
7
Explanation of Sample Input 2 :
For the first test case, the maximum sum of nodes = 2 + 3 = 5
For the third test case, the maximum sum of nodes = 7.
Hint

Think about the fact that if a parent node is considered then none of its child nodes will be considered and vice versa.

Approaches (2)
Using Memoization

Keeping in mind the fact that both node and its children can not be considered for the maximum sum at the same time, we know that if we take a node into our sum, then we will directly call recursively for its grandchildren, OR if we don't take the node into our consideration, we will call for its child nodes and finally consider the maximum sum from both these results.

 

Considering the above idea, we now think about making a working approach to this problem. The drawbacks of the above idea are that it can lead to solving the same subproblems multiple times. 

 

For example: Consider this binary tree:

Now, here when we choose the root node ‘1’, it will call its grandchild nodes ‘4’ and ‘5’. Similarly when we move to child node ‘3’ and do not select it, then again the nodes ‘4’ and ‘5’ will be called child nodes of ‘3’. This leads to processing nodes ‘4’ and ‘5’ more than once. 

 

    In order to stop solving these nodes more than one time, we will memorize the result at each node.  

 

In order to solve this problem, we will use an unordered_map for memoizing the result which stores the result of the complete subtree rooted at a node in the unordered_map, so that if we call the same node again, instead of calculating the value again, we can directly return the value stored in the map.

 

Algorithm:

 

  1. Create a function that returns the maximum sum of nodes from the subset of nodes of the Binary tree under certain given conditions. Create an unordered_map that stores the result of subtree sum.
  2. Create a function that returns maximum sum rooted at a certain node ‘node’
    • If the node = 0, simply return 0
    • Check if node is already processed:
      • If yes, return the calculated value from the map
      • If no, move forward
    • Take the current node value and recursively call for all its grandchild nodes and store the value in a variable say “node_included”
    • Now, don’t take the current node value and hence, recursively call for all its child nodes and store it in a separate variable say “node_not_included”
    • Now, finally choose the maximum of “node_included” and “node_not_included” values and store it in the map.
    • Return map.
Time Complexity

O(N), Where ‘N’ is the number of nodes in the given binary tree.

 

Since we are visiting each node exactly once, and at each function call, we are checking if the node is already processed or not, the overall time complexity is O(N).

Space Complexity

O(N), Where ‘N’ is the number of nodes in the given binary tree.

 

Since we are storing the results of each node in a map, the space complexity required for creating an unordered_map, makes the space complexity to be O(N).

Code Solution
(100% EXP penalty)
Maximum Sum Of Nodes
Full screen
Console