Maximum Sum Path Of A Binary Tree.

Hard
0/120
Average time to solve is 25m
profile
Contributed by
60 upvotes
Asked in companies
HikeSamsungDirecti

Problem statement

You are given a binary tree having 'n' nodes. Each node of the tree has an integer value.


Your task is to find the maximum possible sum of a simple path between any two nodes (possibly the same) of the given tree.


A simple path is a path between any two nodes of a tree, such that no edge in the path is repeated twice. The sum of a simple path is defined as the summation of all node values in a path.

Detailed explanation ( Input/output format, Notes, Images )
Input Format 
The only line of input contains elements in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image would be :

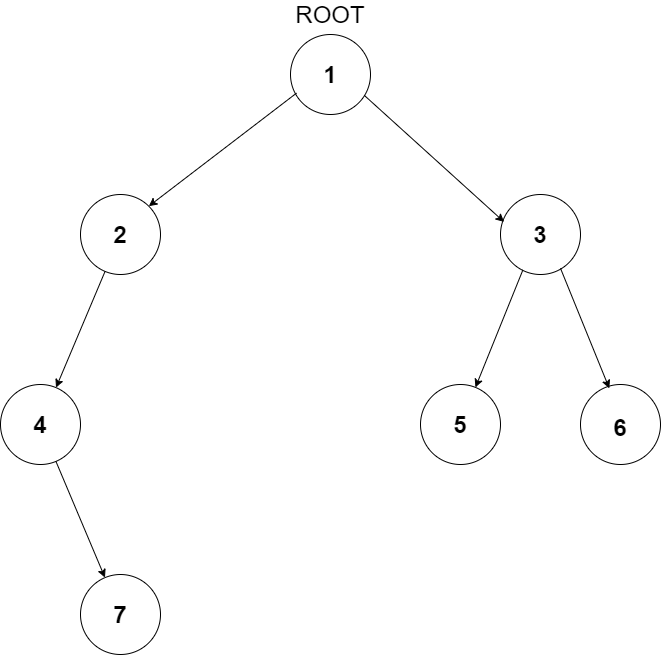
Example Input

1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :

Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level, and so on.
The input ends when all nodes at the last level are null(-1).
Note : 
The above format was just to provide clarity on how the input is formed for a given tree. 
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format: 
Print the maximum sum of a simple path between any two nodes of the given tree.
Note: 
You don’t need to print anything; It has already been taken care of.
Sample Input 1:
1 2 3 4 -1 -1 -1 -1 -1
Sample Output 1:
10
Explanation For Sample Input 1:
The tree looks as follows:
                        1
                       / \
                      2   3 
                     /
                    4
The path between Node 3 (with value 3) and Node 4 (with value 4) produces the maximum sum, i.e., 10. Hence, the maximum possible sum is 10 in this case.
Sample Input 2:
2 4 -1 3 6 -1 -1 -1 -1
Sample Output 2:
13
Explanation For Sample Input 2:
The tree looks as follows:
                        2
                       / 
                      4    
                     / \   
                    3   6
The path between Node 3 (with value 3) and Node 4 (with value 6) produces the maximum sum, i.e., 13. Hence, the maximum possible sum is 13 in this case.
Expected time complexity:
 The expected time complexity is O(n).
Constraints:
1 <= 'n' <= 10^6
-10^5 <= 'data' <= 10^5 and 'data' !=-1

Where ‘n’ is the total number of nodes in the binary tree, and 'data' is the value of the binary tree node

Time Limit: 1 sec
Hint

Try to think of a recursive approach to solve the problem.

Approaches (1)
Recursive Solution

First of all, we need to observe that for any simple path in a Binary tree, there is one and only one node at the maximum height. So, the idea is to fix each node as the highest node in a path and then find the maximum sum path having the current node as the highest node. The final answer will be the maximum value among all the path sum values for each node. To find the maximum sum path for a particular node as the highest node, we can write a recursive function that finds the maximum sum path between the current node and the descendants in its left subtree and the right subtree respectively. 

 

Steps: 

  1. Let maxSum be a variable that stores the maximum path sum among all paths. Initialize it as INT_MIN. 
  2. Let currentPathSum be a recursive function that takes a node currentPeak as a parameter, and returns the maximum sum path between the currentPeak node and its descendants.
    • If the currentPeak Node is NULL, then we will return 0. This is the base case of the recursive function.
    • Otherwise we will call the recursive function for the left child and right child of currentPeak Node. Let the values returned by them be maxPathSumLeft and maxPathSumRight, respectively.
    • If maxPathSumLeft is negative, then set maxPathSumLeft to 0. As it is better not to consider the left child.
    • If maxPathSumRight is negative, then set maxPathSumRight to 0. As it is better not to consider the right child.
    • Initialize currentSum be the sum of maxPathSumLeft, maxPathSumRight, and the value on currentPeakNode. Here, we are storing the maximum path sum for a node having currentPeakNode as the topmost node.
    • Update maxSum to the maximum value among currentPathSum and maxSum.
    • Return the summation of value on currentPeakNode and the maximum value among maxPathSumLeft and maxPathSumRight. This will be used for calculating the maximum sum path value for the parent nodes.
  3. Call the recursive function currentPathSum, for the root node of the tree.
  4. Return the maxSum variable.
Time Complexity

O(N), where N is the number of nodes in the given binary tree.

 

As we are visiting each node of the binary tree only once. Hence, the overall Time Complexity is O(N).

Space Complexity

O(N), where N is the number of nodes in the given binary tree.

 

In the worst case, when the given tree is a skewed tree. The recursion stack depth will be N. Hence, the overall Space Complexity is O(N).

Code Solution
(100% EXP penalty)
Maximum Sum Path Of A Binary Tree.
Full screen
Console