Problem

Submissions

Hints & solutions

Discuss

Maximum Sum Rectangle

Easy

0/40

Average time to solve is 15m

Contributed by

235 upvotes

Asked in companies

Problem statement

You are given a matrix ‘ARR’ with ‘N’ rows and ‘M’ columns. Your task is to find the maximum sum rectangle in the matrix.

Maximum sum rectangle is a rectangle with the maximum value for the sum of integers present within its boundary, considering all the rectangles that can be formed from the elements of that matrix.

For Example

Consider following matrix:

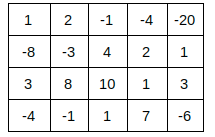
The rectangle (1,1) to (3,3) is the rectangle with the maximum sum, i.e. 29.

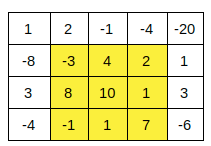
Detailed explanation ( Input/output format, Notes, Images )

Input Format

The first line of input contains an integer ‘T’ denoting the number of test cases to run. Then the test cases follow.

The first line of each test case contains two space-separated integers ‘N’ and ‘M’ denoting the number of rows and number of columns respectively.

The next ‘N’ lines contain ‘M’ space-separated integers denoting the elements of ARR.

Output Format

For each test case, print the value of the sum for the maximum sum rectangle.

Print the output of each test case in a separated line.

Note

You do not need to print anything; it has already been taken care of. Just implement the given function.

Constraints

 1 <= T <= 10
 1 <= M, N <= 75
 -10^5 <= ARR[i][j] <= 10^5

Time Limit: 1 sec

Sample Input 1

Sample Output 1

1
4

Explanation of Input 1

The maximum sum rectangle corresponding to the first test case is-

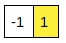
The maximum sum rectangle corresponding to the second test case is-

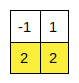
Sample Input 2

1
4 5
1 2 -1 -4 -20
-8 -3  4 2 1
3  8 10 1 3
-4 -1 1 7 -6

Sample Output 2

Hint 1

Hint 2

Hint 3

Can we iterate over all possible rectangles?

Approaches (3)

Approach 1

Approach 2

Approach 3

Brute Force

We will iterate through all the rectangles of the matrix with the help of nested loops and return the maximum sum found.

Algorithm

We will iterate over the ‘leftBoundary’, ‘rightBoundary’, ‘upBoundary’, ‘ ‘downBounday’ of the rectangle with the help of four nested loops.
For each of the boundaries, we will find the sum of the rectangle contained in it.
We finally return the maximum obtained sum.

Time Complexity

O((N * M) ^ 3), where N denotes the number of rows of the matrix and M denotes the number of columns of the matrix.

We will iterate over all the boundaries of the rectangle in O((N * M) ^ 2) time. For each rectangle, we are finding out its sum in O(N * M) time.

Hence, overall time complexity will be O((N * M) ^ 2 * (N * M)) = O((N * M) ^ 3).

Space Complexity

O(1)

Constant space is used.

(75% EXP penalty)

(100% EXP penalty)

Maximum Sum Rectangle

Console