Problem
Submissions
Hints & solutions
Discuss
Minimize Cash Flow
Easy
0/40
Average time to solve is 15m
Problem statement
You are given a list of ‘transactions’ between ‘n’ number of friends. who have to give each other money. The list consists of data of receiver, sender, and transaction.
Your task is to minimize the cash flow and the total number of transactions should also be minimum.
For example :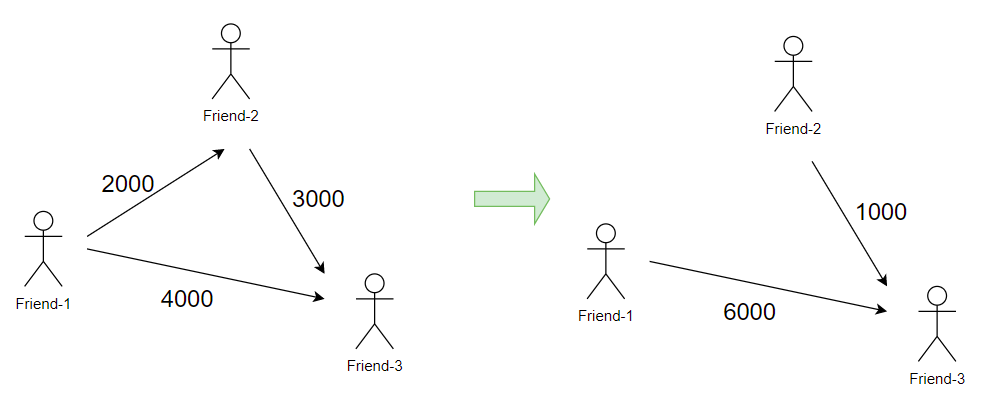
In figure 1 : friend-1 has to pay 2000$ to friend-2, and 4000$ to friend-3 and friend-2 has to pay 3000$ to friend-3.
In figure 2 : so we can minimize the flow between friend-1 to friend-2 by direct pay to friend-1 to friend-3
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line of input contains a number ‘T’ denoting the number of test cases.
The first line of each test case contains two space-separated integers ‘n’, where ‘n’ denotes the number of friends.
The next ‘n’ line consists of ‘n’ space-separated number, where ‘i’, ‘j’ represents the ‘i-th’ friend to pay ‘arr[i][j]’ to ‘j-th’ friend.
For every test case, return the 2-D matrix.
Output for each test case will be printed in a separate line.
You do not need to print anything; it has already been taken care of. Just implement the given function.
1 <= T <= 5
1 <= N <= 1000
0 <= arr[i][j] <= 10^9
Time Limit: 1 sec
Sample Input 1 :
2
4
0 100 0 200
0 0 300 0
0 0 0 200
0 0 0 0
3
0 2000 4000
0 0 3000
0 0 0
Sample Output 1 :
0 0 0 300
0 0 100 100
0 0 0 0
0 0 0 0
0 0 6000
0 0 1000
0 0 0
Explanation For sample input 1 :
Test Case 1 :
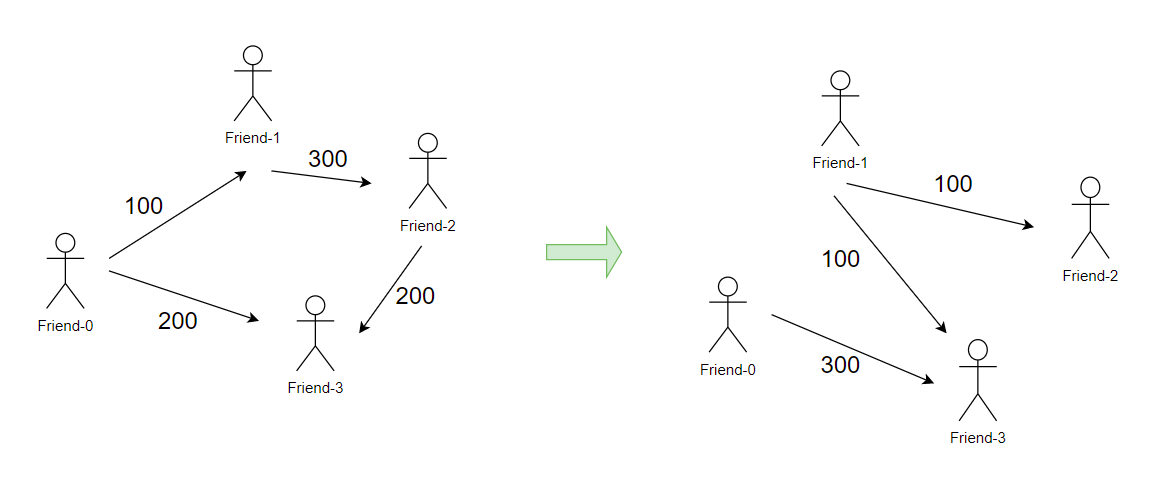
As you can see: friend-0 has to pay only 300$ to friend-3, friend-1 has to pay 100$ to friend-2 and 100$ to friend-3.
So output will be
0 0 0 300
0 0 100 100
0 0 0 0
0 0 0 0
Test Case 2 :
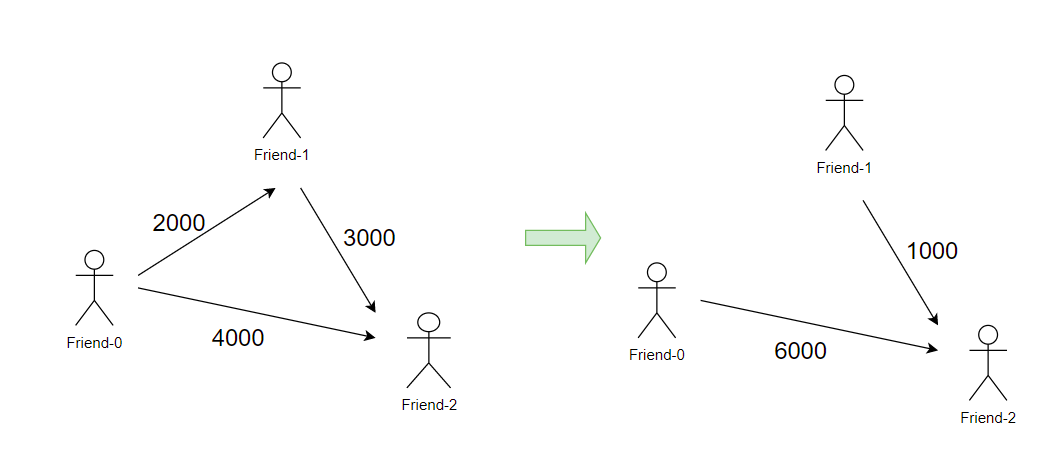
As you can see: friend-0 has to pay only 600$ to friend-2, friend-1 has to pay only 1000$ to friend-2.
So output will be
0 0 6000
0 0 1000
0 0 0
Sample Input 2 :
2
3
0 100 0
0 0 200
0 0 0
3
0 100 0
0 0 100
100 0 0
Sample Output 2 :
0 0 100
0 0 100
0 0 0
0 0 0
0 0 0
0 0 0
Hint
Hint 1
Think in a greedy manner.
Approaches (1)
Approach 1
Greedy
We can calculate the net amount of every person as-
Net amount = sum of all received money - the sum of all sent money.
Find the person with the maximum and the minimum net amount, suppose ‘x’ person has maximum net amount ‘maxAmount’ and ‘y’ person has a minimum amount ‘minAmount’, then ‘y’ person will pay ‘minAmount’ to ‘x’ person after this transaction net amount of ‘x’ person is ‘maxAmount = maxAmount - abs( minAmouny ), and the net amount of ‘y’ person is ‘0’,
Repeat this process until all the amount will not settle or ‘0’.
Algorithm-
- Create a net amount array ‘netAmount’
- Fill this array, Now for every friend ‘i’
- ‘netAmount[i]’= sum of all received money by ‘i-th’ friend - the sum of all sent money by ‘i-th’ friend.
- Create a 2-D matrix to store the ‘answer’.
- Iterate a while loop until all the values of ‘netAmount’ is not ‘0’
- Find the minimum and maximum of ‘netAmount’
- Suppose ‘x’ index value is the max net amount and ‘y’ index is min net amount, then:
- ‘netAmount[x] = netAmount[x]- abs( netAmount[y] )’
- Update ‘answer[y][x] = abs( netAmount[y] )
- It represents that the ‘y-th’ friend will pay ‘netAmount[y]’ to ‘x-th’ friend.
- Set ‘netAmount[y] = 0’.
- In the end, return ‘answer’.
Time Complexity
O(N ^ 2), Where ‘N’ is the number of friends.
We are iterating a two nested loop of size ‘N’ and ‘N’, first one until all the values are not ‘0’, second to find min-max of ‘netAmount’ array.
Space Complexity
O(N ^ 2), Where ‘N’ is the number of friends.
We are storing our answer in another 2-d matrix called ‘answer’.
Code Solution
(100% EXP penalty)
Minimize Cash Flow
C++ (g++ 5.4)
Console




