Minimize Malware Spread II

Hard
0/120
Average time to solve is 30m
profile
Contributed by
22 upvotes
Asked in companies
Flipkart limitedalibaba

Problem statement

You are given a network of ‘N’ nodes numbered from 0 to ‘N-1’. This network is represented using an adjacency matrix ‘GRAPH’ of size ‘N’ x ‘N’. You are also given an array ‘INITIAL’ of size ‘M’, which contains the nodes that are initially infected by malware. If there is a direct connection between two nodes and at least one of them is infected by malware, both nodes will be infected by the malware. This malware spread will continue until no more nodes are left, or no more nodes can be infected by this manner.

Let us define a variable ‘INFECTED’ to the total number of infected nodes by the malware spread. Your task is to remove exactly one node from the array ‘INITIAL’ such that it results in the ‘minimum’ value of ‘INFECTED’.

Note :

1. If GRAPH[X][Y] = 1, then the node ‘X’ is directly connected to a node ‘Y’. Otherwise, there is not a direct connection between ‘X’ and ‘Y’.
2. If we remove a node, we must also remove its connections to any other node.
3. If multiple such nodes exist that can minimize the value of ‘INFECTED’, you have to find the node with the smallest index.
4. All nodes in the array ‘INITIAL’ are unique.
5. You have to return the ‘index’ of the node, not the minimum value of the ‘INFECTED’.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains an integer ‘T’, which denotes the number of test cases to be run. Then, the T test cases follow. 

The first line of each test case contains two positive integers, ‘N’ and ‘M’, denoting the number of nodes in the network and the number of initially infected nodes respectively.

The following ‘N’ lines of each test case contain ‘N’ integers each, representing the adjacency matrix ‘GRAPH’.

The last line of input contains ‘M’ space-separated non-negative integers, denoting the elements of the array ‘INITIAL’.
Output Format : 
For each test case, print the ‘index’ of the node that, after removing, would minimize the value of ‘INFECTED’, as described in the problem statement.

Output for each test case will be printed in a separate line.
Note : 
You do not need to print anything. It has already been taken care of. Just implement the given function.
Constraints : 
1 <= T <= 5
2 <= N <= 100
0 <= GRAPH[i][j] <= 1,  GRAPH[i][j] == GRAPH[j][i]
GRAPH[i][i] == 1
1 <= M <= N
0 <= INITIAL[i] < N

Time Limit: 1sec
Sample Input 1 :
1
3 2
1 0 1
0 1 1
1 1 1
0 2
Sample Output 1 :
2
Explanation For Sample Input 1 :

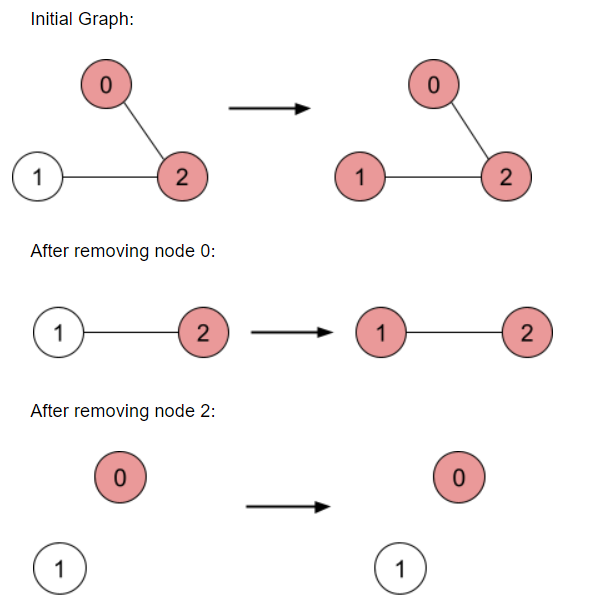
altImage

The left side graph denotes the initial nodes infected by malware, and the right side indicates the final graph after malware spread.
If you remove node ‘2’ from the ‘INITIAL’, you will get the minimum value of ‘INFECTED’ that is 1. There is no other way to get a value of ‘INFECTED’ less than 1.
Sample Input 2 :
1
3 1
1 0 1
0 1 1
1 1 1
0
Sample Output 2 :
0
Explanation For Sample Input 2 :
There is only one node in the array ‘INITIAL’. So, we have to remove it.

altImage

Hint

Use BFS to calculate how many nodes will be infected after removing the ith node from the array INITIAL.

Approaches (2)
BFS Based Approach
  • The idea here is to use the BFS to calculate how many nodes will be infected after removing the ith node from the array INITIAL.
  • So, we have to run the BFS for each node in the initial array.
  • First, create a HashSet named infectedNodes that contains all initially infected nodes.
  • Declare a variable ans to store the final answer, initialize it with 0.
  • Also, declare a variable minCount to store the minimum value of INFECTED, initialize it with INT_MAX.
  • Now, we have to traverse through the array initial, let it be cur, in each iteration do:
    • Remove the node cur from the array initial, and from the graph itself, infectedNodes.remove(cur).
    • Call the function bfs and pass graph, infectedNodes, and cur. It returns the number of nodes that are infected after the malware spread. Let the return value of this function is store in the variable cnt.
    • We have to update our ans if the return value of bfs is smaller than minCount, or if equal and index that is cur is smaller than ans.
    • So, if (cnt < minCount or (cnt == minCount and cur < ans), then
      • minCount = cnt.
      • ans = cur.
    • Before completing the current iteration, we must again insert the removed node, i.e., cur, into the HashSet infectedNodes, infectedNodes.insert(cur).
  • Finally, return the ans.

int bfs(int[][] graph, HashSet infectedNodes, int cur):

  • Create a queue named q that will contain all the nodes which are going to be explored.
  • Now, push all the nodes of the HashSet infectedNodes into queue q.
  • Run a while loop until the queue become empty:
    • Store the front element of the queue in the variable v, and also remove it.
    • Run a for loop from i = 0 to i < graph[v].size() to traverse through all the direct connections of node v, in each iteration do:
      • If i != cur and graph[v][i] == 1 and !infectedCount(i), then push i into the queue, and insert the same into the HashSet.
  • Finally, infectedNodes will contain all the infected nodes after the malware spread and after the removal of cur.
  • Return the size of infectedNodes.
Time Complexity

O(N^3), where ‘N’ is the number of nodes.

 

The time complexity of the BFS using the adjacency matrix is O(N^2), and we are calling BFS for each node in the array ‘INITIAL’. Hence, the overall time complexity will be O(N^3).

Space Complexity

O(N), where ‘N’ is the number of nodes.

 

As we are creating a HashSet that will contain all the infected nodes, which can go up to N only.

Video Solution
Unlock at level 3
(75% EXP penalty)
Code Solution
(100% EXP penalty)
Minimize Malware Spread II
Full screen
Console