Minimum Travel Cost

Moderate
0/80
Average time to solve is 40m
profile
Contributed by
9 upvotes
Asked in companies
AmazonSamsungErnst & Young (EY)

Problem statement

Ninjaland is a country having 'N' states numbered from 1 to 'N'. These 'N' states are connected by 'M' bidirectional roads. Each road connects to different states and has some cost to travel from one state to another. Now, the chief wants you to select 'N' - 1 roads in such a way that the tourist bus can travel to every state at least once at minimum 'COST'.

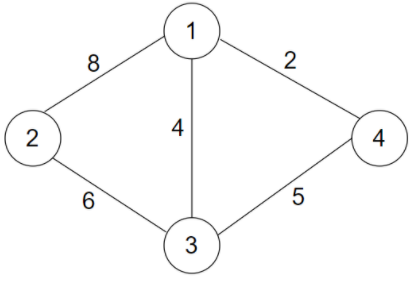
For example : 
Consider a country having 4 states numbered from 1 to 4. These 4 states are connected by 5 bidirectional roads given as :
1 --- 2 with cost = 8
2 --- 3 with cost = 6
3 --- 4 with cost = 5
1 --- 4 with cost = 2
1 --- 3 with cost = 4

The map of the country can be represented as:


Now, the best way to choose 3 roads is:


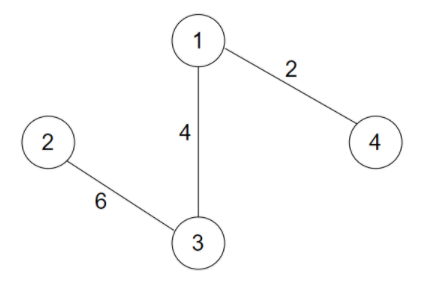
The cost of travelling from any state to all other states is  2 + 4 + 6 i.e. 12.
Detailed explanation ( Input/output format, Notes, Images )
Input format : 
The first line contains an integer 'T' denoting the number of test cases or queries to be run. 

The first line of each test case or query contains two space-separated integers 'N' and ‘M’ representing the number of states and number of roads in the country, respectively. 

The next 'N' lines of every test case contain three single space-separated integers ‘A’, ‘B’ and ‘C’, representing a road between the states 'A' and 'B' and 'C' denoting the cost of travelling them.
Output format: 
For each test case, print 'N' - 1 lines each containing 3 space separated integers 'A', 'B' and 'C' representing the road you have chosen and the cost to traverse that road.
Note: 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
1 <= 'T' <= 10
1 <= 'N' <= 1000
'N' - 1 <= 'M' <= 2000
1 <= 'C' <= 10^6 

Time limit: 1 sec
Sample Input 1:
1
4 4
1 2 3
1 4 5
2 3 1
3 4 8
Sample Output 1 :
1 2 3
2 3 1
1 4 5
Explanation for 1:
Here 'N' = 4, So we need to pick 3 roads such that all states are visited and cost is minimum. Now the possible ways are.

1. (1, 2) (2, 3) (1, 4): In this case, the total cost of travelling is 3 + 1 + 5 = 9.
2. (1, 2) (2, 3) (3, 4): In this case, the total cost of travelling is 3 + 1 + 8 = 12.
3. (1, 2) (1, 4) (3, 4): in this case, the total cost of travelling is 3 + 5 + 8 = 16.
4. (1, 4) (2, 3) (3, 4): In this case, the total cost of travelling is 5 + 1 + 8 = 14.

Clearly, the cost is minimal in the first case so we pick (1, 2) ( 2, 3) (1, 4) with cost of travel 9. Refer above for diagram.
Sample Input 2:
1
3 3
1 2 5
2 3 4
3 1 2
Sample Output 2 :
2 3 4
3 1 2
Explanation for 2:
The given graph is:


Here 'N' = 3, So we need to pick 2 roads such that all states are visited and the cost is minimum. Now the possible ways are.

1. (1, 2) (2, 3) : In this case, the total cost of travelling is 5 + 4 = 9.
2. (1, 3) (2, 3) : In this case, the total cost of travelling is 2 + 4 = 6.
3. (1, 2) (1, 3) : in this case, the total cost of travelling is 5 + 2 = 7.

Clearly, the cost is minimal in the second case so we pick (1, 3) ( 2, 3)  with the cost of travel 6.

Hint

The problem wants us to find a minimum spanning tree for the country. So, the idea is to use Prim’s algorithm to find the minimum spanning tree.

Approaches (2)
Using Adjacency Matrix

The idea is to create a graph of the country with states as its vertices and roads as edges. 

For creating a graph we will use an adjacency matrix representation of graph Cost with Cost[i][j] representing the cost of travelling from state i to state j and vice versa, state j to i.

The very first approach to solve this problem is using Prim’s algorithm, which is a greedy algorithm.

 

The idea behind Prim’s algorithm is simple, a spanning tree means all states must be connected.

  • Firstly, we start with an empty spanning tree.
  • We bifurcate the states in 2 groups:
    • The first group contains the states already included in the MST.
    • The other group contains the states not yet included.
  • At every step, it considers all the roads that connect the two groups and picks the minimum weight road from these roads or minimum weight state from the second group.
  • After picking the road, it adds the state of the second group into the first group ( MST group).

 

Algorithm:

  1. Firstly, create an adjacency matrix of the given roads and costs.
  2. Create a visited array of size N that keeps track of states already included in MST. Initially mark all states as unvisited.
  3. Create a weight array of size N, to assign a weight value to all states in the input graph. Initialize all weight values as INFINITE. Assign the weight value as 0 for the first state so that it is picked first.
  4. While all states are not visited.
  • Pick a state A which is not marked as visited and has a minimum weight value.
  • Include A to visited.
  • Now follow these steps:
    • For each i from 1 to N :
      • If there is a path between A and i such that i is not marked as visited and weight of i is less than cost of road:
        • Update weight[i] = cost of road A - i.

Let’s understand with the example : 

Initially, all the states are marked unvisited and weight values of states are {0, INF, INF, INF}. 

Now, pick the state with minimum weight. i.e. state 1 and mark it as visited. 

After picking this state, update the weight values of all adjacent states of 1, which are 2 and 4 in this case to their corresponding costs.

The weight array becomes: {0, 3, INF, 5}.

 

 

Now, pick the next state with minimum weight which is not visited yet. i.e. state 2 and mark it as visited. 

After marking state 2 visited, update the weight value of all the adjacent states of 2 which are not visited yet, i.e state 3 to their corresponding cost if and only if it is less than the one stored in the weight array. 

The weight array becomes; {0, 3, 1, 5}.

Similarly, pick the next unvisited state with minimum weight i.e. 3 and mark it as visited.

Update weight values of adjacent states of state 3 which are not visited  to their corresponding cost if and only if it is less than the one stored in the weight array. 

In the above point, the adjacent states of 3 are 4 and 2.

  1. We need not interfere with state 2 as it is already visited.
  2. In case of state 4, weight[4] is less than cost [3 to 4] i.e. 5 < 8, thus, we don’t update.

So, the final MST we get is,


 

Time Complexity

O(N ^ 2) per test case where N is the number of states in the country. 

 

In the worst case, we are looking at the weight values of all states to get a minimum weight state, this step takes O(N) and we perform these operations N-1 times.

Space Complexity

O(N ^ 2) per test case where N is the number of states in the country. 

 

We are creating an adjacency matrix representation of the given country.

Code Solution
(100% EXP penalty)
Minimum Travel Cost
Full screen
Console