Minimum Cost

Easy
0/40
Average time to solve is 15m
profile
Contributed by
2 upvotes
Asked in companies
IBMQualcommDunzo

Problem statement

There are ‘N’ numbers of balls in a room that are placed in a row. You are given an array ‘location’ where location[ i ] denotes the location of the ‘i-th’ ball.

You have to move all the balls at the same location, and it is given that you can move a ball from position [ i ] to

1. position[i] + 2 with cost = 0.

2. position[i] + 1 with cost = 1.

Your task is to find the minimum cost required to move all the balls at the same location.

For Example : 
If we have three balls placed at [ 1, 3, 4 ]


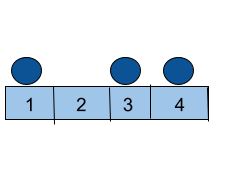
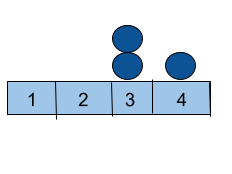
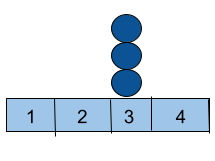
At first, move the ball from position ‘1’ to position ‘3’ with cost = 0.
Then move the ball from position ‘4’ to position ‘3’ with cost =1.
As the minimum cost = 1, so you need to print 1.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains a single integer ‘T’ denoting the number of test cases.

Each test case’s first line contains a single integer ‘N’, denoting the number of balls.

The second line of each test case contains ‘N’ space-separated integers denoting the balls’ positions.
Output Format : 
For each test case, print a single integer denoting the minimum cost required to move all the balls to the same location.

Print the output of each test case in a separate line.
Note : 
You don’t need to print anything. It has already been taken care of. Just implement the given function.
Constraints : 
1 <= T <= 50
1 <= N <= 10^5
1 <= location[i] <= 10^5

Where location[i] is the location of the ‘i-th’ ball.

Time limit: 1 sec.
Sample Input 1 :
2
4
3 5 6 8
3
4 4 4
Sample Output 1 :
2
0
Explanation Of Sample Input 1 :
Test Case 1: Moving the ball at position ‘5’ to position ‘3’ cost = 0.
Moving the ball from position 8 to 3 costs = 1.
Moving the ball from position 6 to 3 costs = 1.
So the total cost is ‘2’ and this is the minimum cost.

Test Case 2: All the balls are already at the same location so the minimum cost = 0.
Sample Input 2 :
2
6
3 8 6 9 14 10
4
5 10 13 4
Sample Output 2 :
2
2
Hint

Try to move all odd positioned balls at one place and all even positioned balls at one place.

Approaches (1)
Naive Approach

As moving the ball at location[ i ] to location[ i ] + 2 and location[ i  ] - 2  does not cost anything. 


So it can be noted that we can move any ball at an even position to any other even position with ‘0’ cost.

And any ball at an odd position to some other odd position with ‘0’ cost.


Now we can move all the balls at even position to ‘0’ and all the balls at the odd position to ‘1’ with no cost.


Now we have to pile all the balls either at ‘0’ or at ‘1’. 

Cost of moving all the balls from 0 to 1 = number of balls at 0 i.e number of balls that were at even positions.

Cost of moving all the balls from 1 to 0 = number of balls at 1 i.e number of balls that were at odd positions.


So the minimum cost to move the balls at the same location will be the minimum of the count of balls at even position and count of balls at odd positions.


Algorithm

 

  • Initialize two variables ‘odd’ and ‘even’ with values ‘0’ to store the count of balls at odd and even positions respectively.
  • Iterate through the ‘location’ array, i: 0 to N-1
    • If location[ i ] is even.
      • Increment ‘even’.
    • Otherwise
      • Increment ‘odd’.
  • Return minimum of ‘odd’ and ‘even’.
Time Complexity

O(N), where ‘N’ is the length of the ‘location’ array.


We are iterating through the array once. Therefore the time complexity is O(N).

Space Complexity

O(1)

 

We have not used any extra space. So space complexity is O(1).

Code Solution
(100% EXP penalty)
Minimum Cost
Full screen
Console