Minimum Knight Moves

Hard
0/120
profile
Contributed by
20 upvotes
Asked in companies
MathworksAmazonRupeek

Problem statement

You are given an infinite chessboard (ie: the x-coordinates and y-coordinates can be anything between -infinity to +infinity).

You have a knight placed at coordinates ‘(0, 0)’. Find the minimum number of steps needed to move the knight to ‘(X, Y)’.

The knight has 8 possible moves, each move is two units in a cardinal direction, then one unit in an orthogonal direction.

For example :

As depicted in the photo below, the knight currently at (0, 0) can move to any of the 8 positions: (1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1), (-2, 1), (-1, 2).

Example : 
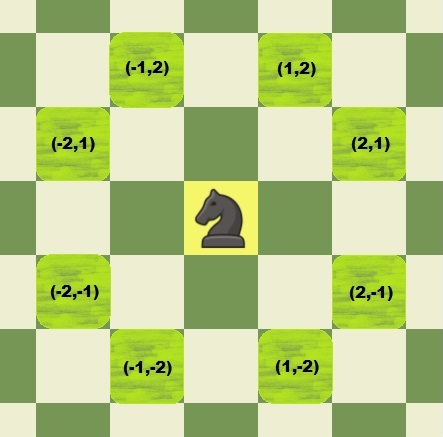
If X = 1 and Y = -1, then we need to find out the minimum number of steps to move the knight from (0, 0) to (1, -1).

We need at least 2 steps to move the knight to the desired position.

First move: (0, 0) -> (2, 1) 

Second move: (2,1) -> (1, -1)

Here we can see that there are many ways, but we need at least 2 steps. Therefore we will return the value 2.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains a single integer ‘T’ denoting the number of test cases, then each test case follows:

The first and only line of each test case contains two integers ‘X’ and ‘Y’, denoting the x-coordinate and y-coordinate of the final position of the knight.
Output Format : 
For each test case, print the minimum number of steps needed.

Output for each test case will be printed in a separate line.
Note : 
You are not required to print anything; it has already been taken care of. Just implement the function.
Constraints : 
1 <= T <= 10      
-100 <= X, Y <= 100

Time limit: 1 sec
Sample Input 1 :
2
1 1
1 0
Sample Output 1 :
2
3
Explanation For Sample Input 1 :
For test case 1 :
(0, 0)  to (2, -1) to (1,1), therefore 2 steps are required. The other possible way is (0, 0) to (-1, 2) to (1, 1), but we require at least 2 steps to move from (0,0) to (1,-1). 

Hence return value 2. Refer the image for better understanding:


For test case 2 :
(0, 0) to (2, 1) to (0, 2) to (1, 0), therefore 3 steps are required. Refer the image for better understanding:

Sample Input 2 :
2
12 5
5 12
Sample Output 2 :
7
7
Hint

Can you take advantage of the small constraints and simulate the moves? Also try finding some symmetry.

Approaches (3)
Breadth-First Search With Pruning

There is symmetry because of how the knight moves, this leads us to the conclusion that the steps required to reach (x, y), (-x, y), (y, -x) and (-x, -y) are the same. We can narrow down our search space to just the first quadrant (ie: the final target position now becomes (abs(x), abs(y)).


One of the most intuitive ways to solve this is by using breadth-first search (bfs). We can simulate the moves, simply start by pushing position (0, 0) into a bfs-queue. Also maintain a hash-map to store the visited positions on the chessboard as this hash-map will store the minimum moves to reach that particular position. Similar to the standard bfs approach, start exploring the next positions that can be reached and push them into the bfs-queue if they are still unexplored. Finally when we reach the target position return the value of minimum moves.

 

Important: Are you getting TLE even after doing everything right? Probably you are visiting many unwanted coordinates causing increased execution time. Think of how can you prune the search? 
If we are going 2 units beyond the x-coordinate/ y-coordinate then we no longer need to search beyond that, surely a shorter path will exist in some other way. So don't push coordinates into bfs-queue if they are violating this.


The steps are as follows :

 

  • Take the absolute value of x-coordinate and y-coordinate to narrow down the search to the 1st quadrant.
  • Initialize queue for the bfs-traversal, and also declare a container vis to store the positions already visited.
  • Declare an array “moves” so that you can easily stimulate and check for the next positions.
  • Push (0, 0) into q and set the mark (0, 0) as visited.
  • Apply standard bfs, run the while loop till the q is non-empty or the target position is not reached.
  • Each time, push the elements that will be visited in the next move into q and also mark them as visited in vis.
  • Remember: you need to apply pruning to avoid visiting the unwanted coordinates to save the run-time.
  • Finally, return the minimum steps to reach the target position.
Time Complexity

O( | X * Y | ), where X and Y denote the final x-coordinate and y-coordinate.


As we are exploring each position maximum of 1 time, thus the time required to execute is directly proportional to the number of positions we need to explore. In the worst case, we might have to explore all the cells lying between inside a big square whose ends of diagonal are (0, 0) and (X, Y), area of this square is ~X*Y.  

 

Hence the time complexity is O(|X*Y|).

Space Complexity

O( | X * Y | ), where X and Y denote the final x-coordinate and y-coordinate.


We are storing the minimum steps needed to reach all the visited squares. As the visited squares can be of order ~X*Y. 

 

Hence the space complexity is O(|X*Y|).

Code Solution
(100% EXP penalty)
Minimum Knight Moves
Full screen
Console