Problem
Submissions
Hints & solutions
Discuss
Minimum Number Of Moves To Get All Keys
Moderate
0/80
Average time to solve is 25m
Problem statement
Some players are put inside an ‘N’ x ‘M’ matrix ‘GRID’ one by one where:
- ‘.’ represents an empty cell.
- ‘#’ represents a wall.
- ‘@’ represents the starting point.
- Lowercase letters represent keys.
- Uppercase letters represent locks.
The player to collect all the keys in minimum moves will win the game. The ninja is one of the players and needs your help to win the game. He wants you to find the minimum number of moves to get all the keys. The rules of the game are:
- You have to start from the starting point and move in one of the four cardinal directions.
- You cannot walk outside the grid or walk into a wall. You can pick a key whenever you walk over it.
- You cannot walk over a lock unless you have the corresponding key. For example, the key for the lock ‘A’ is ‘a’.
- There is exactly one key for each lock.
For Example:
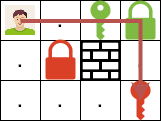
You are given ‘GRID’= [[“@.aA”],[“.B#.”],[“...b”]]. Then the answer will be 5.
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line of the input contains a single integer 'T', representing the number of test cases.
The first line of each test case contains an integer ‘N’, representing the number of rows in ‘GRID’.
The next ‘N’ lines contains a String, representing a row of the ‘GRID’.
For each test case, print the minimum number of moves to get all the keys. Print -1 if it is impossible to get all keys.
Print the output of each test case in a separate line.
You do not need to print anything. It has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 10
1 <= N <= 100
1 <= M <= 100
GRID[i][j] is either an English letter, ‘.’, ‘#’, or ‘@’.
Each key is unique.
Each key has a matching lock.
Alphabets for the keys and locks are chosen in the same order as English alphabets.
The number of keys is in the range [1, 6].
Time Limit: 1 sec
Sample Input 1:
2
3
@.aA
.B#.
...b
1
@BaAb
Sample Output 1:
5
-1
Explanation of Sample Input 1:
For the first test case, then the answer will be 5.

For the second test case, the answer will be -1.

Sample Input 2:
2
2
@.ba
.AB.
1
@.aAbB
Sample Output 2:
3
4
Hint
Hint 1
Try to find the shortest path to get all keys.
Approaches (1)
Approach 1
Breadth-First Search
Prerequisite: Breadth-First Search, Dp & Bit-masking
In this approach, we will use BFS to get the shortest path to get all the keys. We will start from the starting position and move in all four cardinal directions. We use a queue to perform BFS. The BFS queue will store the next possible states for any state. Each time we move to the next state, we will increment the number of moves. When we have collected all the keys, we will stop our BFS and return the number of moves. To prevent revisiting any state, we will use a 3d array to track visited states.
What is the state?
A state has three fields (x, y, key). (x, y) are the coordinates of a cell in the grid, and key is the number of keys we have in this state.
How to confirm if all keys are collected?
To confirm if all the keys are collected, we use the concept of DP & Bit-masking. As the alphabets are chosen in the same order as the English alphabets, we will have a variable ‘MAX’ with us, which will help us to check if we have collected all keys or not. For example, if the max alphabet is ‘c’, our max will be 4. We will represent each alphabet as a bit in the integer keys. We get ‘c’, ‘MAX’ is 100. When we get ‘a’, ‘MAX’ becomes 101. When we get ‘b’, ‘MAX’ becomes 111. Now, if the number of keys of the current state is equal to ((1<<max)-1), then it means we have collected all the keys.
Algorithm :
- Initialize the ‘DX’ and ‘DY’ array to store cardinal directions.
- Set ‘MAX’, ‘X’, and ‘Y’ as 0.
- Iterate ‘I’ in 0 to ‘GRID’:
- Iterate ‘J’ in 0 in ‘GRID[I].LENGTH’:
- If ‘GRID’[‘I’][‘J’] is a key, set ‘MAX’ as the maximum of ‘MAX’ and ‘KEY’.
- If ‘GRID’[‘I’][‘J’] is the starting point, set ‘X’ as ‘I’ and ‘Y’ as ‘J’.
- Iterate ‘J’ in 0 in ‘GRID[I].LENGTH’:
- Initialize a queue ‘Q’’ and a 3d array ‘VISITED’.
- Set ‘MOVES’ as 0.
- Start BFS. Iterate while ‘Q’ is not empty.
- Store the fields of the current state in an integer array ‘CURR’.
- If ‘CURR’ is not null, increment ‘MOVES’ by 1.
- Check if we got all the keys. If yes, terminate the BFS and return moves.
- Store the number of keys in the current state in a variable ‘KEYS’.
- Move in all the four cardinal directions. Iterate ‘I’ in 0 to 4:
- Store the position of the next cell as (‘NEWX’, ‘NEWY’).
- If the next cell is out of the grid or has a wall, continue checking other directions.
- If the next cell has a lock and has not already been visited, check whether we have a key for this lock or not. If we have a corresponding key to this lock, add the next cell to the queue.
- If the next cell has a key and is not already visited, mark its corresponding bit and add the next cell to the queue.
- If the next cell is the starting position or a free walk, just add the cell to the queue if not already visited.
- If we reach this point, it means we cannot collect all the keys. So, return -1.
Time Complexity
O(N * M * 2 ^ K), where 'N' and 'M' are the number of rows and columns of the grid, and 'K' is the number of keys.
The total number of possible states in the worst case is (N * M * 2 ^ K). We may have to visit all the possible states. Hence, the total time complexity is O(N * M * 2 ^ K).
Space Complexity
O(N * M * 2 ^ K), where 'N' and 'M' are the number of rows and columns of the grid, and 'K' is the number of keys.
We may have to store all possible states. Hence, the total space complexity is O(N * M * 2 ^ K).
Code Solution
(100% EXP penalty)
Minimum Number Of Moves To Get All Keys
C++ (g++ 5.4)
Console




