Problem
Submissions
Hints & solutions
Discuss
Minimum time
Moderate
0/80
Average time to solve is 15m
15 upvotes
Asked in companies


Problem statement
You are given an arbitrary graph consisting of V vertices and E edges, a source node (S) and a destination node (D). Every node of the graph has a colour (Red, Blue or Green) associated with it. The cost of travelling from one node to some adjacent node takes 1 second. If you stop at a node for 1 second, you will get a colour ball of the colour of the current node.
You have to find the minimum time taken in order to reach from source to destination node ensuring that the number of balls of each colour is equal and non-zero. The source and destination nodes will always be in different colours.
Note:
1. The given graph is never empty and consists of at least 3 nodes with the colour Red, Green and Blue each.
2. There are no self-loops(an edge connecting a node to itself) in a graph.
3. There are no parallel edges i.e no two nodes are directly connected by more than 1 edge in the given graph.
4. The nodes in the graph are numbered from 1 to V.
5. All the edges in the graph are bidirectional.
6. You can stay at one node for more than 1 second as well, but every second you stay there you will get an additional colour ball of the colour of that node.
7. Number of edges(E) in the graph is always equal to V-1.
8. You can also collect the ball from the destination and the source node itself. Also if you reach the destination without having an equal number of balls for each colour, the time calculated would not be valid.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line of input contains an integer T, the number of test cases.
The first line of each test case contains two space-separated integers V, and E denoting the number of vertices and number of edges in the given graph respectively.
The second line of each test case denotes V space-separated integers (0 / 1/ 2) denoting the colour of vertex i, where 1 <= i <= V and 0 denotes “Red” colour, 1 denotes “Blue” colour and 2 denotes “Green” colour.
From the third line onwards of each test case, the next 'E' lines will denote the edges of the given graph.
Every edge is defined by two single space-separated integers 'a' and 'b', which signifies an edge between node ‘a’ and node 'b'.
The last line of each test case consists of two space-separated integers S and D, denoting the source node and destination node.
Return an integer denoting the minimum time to reach from source node (S) to destination node (D), fulfilling mentioned conditions.
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 10
3 <= V <= 5000
E = V - 1
1 <= a,b <= V
Time Limit: 1 sec
Sample Input 1:
2
6 5
1 0 2 1 2 0
1 2
1 3
3 4
3 5
2 6
6 5
5 4
0 0 1 2 1
1 2
2 3
3 4
3 5
1 5
Sample Output 1:
7
8
Explanation for Sample Input 1:
For the first test case of sample input 2, Source Node, S = 6 and Destination Node, D = 5.
The tree depicted is as follows:
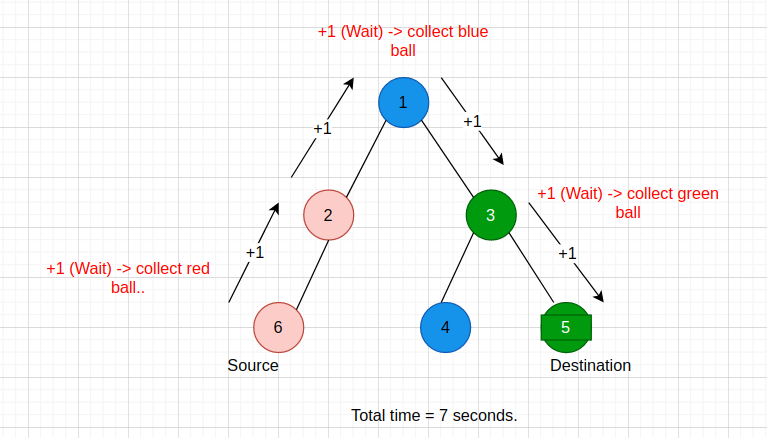
For the second test case of sample input 2, Source Node, S = 1 and Destination Node, D = 5.
The tree depicted is as follows:
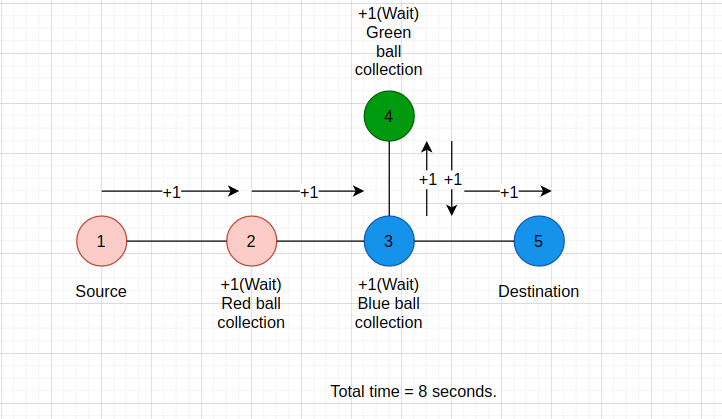
Sample Input 2:
2
5 4
1 0 2 0 0
3 1
4 2
2 3
5 3
2 1
4 3
0 0 2 1
3 2
3 1
3 4
4 3
Sample Output 2:
5
6
Hint
Hint 1
Use Multisource Breadth-First Search to find the minimum distance from the path from source to the destination of the colours.
Approaches (1)
Approach 1
DFS, Linearisation of tree, Multi-source BFS.
The key idea is you will be accepted at the destination node only when you have equal amounts of all three colour balls and the number of coloured balls of each colour (Red, Blue and Green) is always > 0. In other words, it’s wise to take only one coloured ball of each colour before submitting it to the destination node, because if we can reach the destination with 1 ball of each colour then why waste time collecting some extra balls for any colour.
- STORING THE SHORTEST PATH VIA Depth-First Search.
- In this step, we will try to store all the nodes lying in the shortest path between source and destination nodes in the given graph. This step is essential, as in a graph all paths are unique and no matter what the situation is we have to traverse this unique path only in the end.
- Run a Depth-First Search taking source as the root node and maintain a stack of all nodes, Depth-First Search in whose subgraph is not completed yet. If you encounter a destination node, return the stack of all the nodes.
- In the Depth-First Search, mark all the nodes in the shortest path as visited.
- Note that you also need to keep count of red, green and blue nodes in the shortest path from S to D. It is also given that source and destination nodes are of different colours. So, if we can find all the different colour nodes in the path itself, then the answer would be just ‘pathLength + 3(for taking 1 ball of each colour). If a color node is missing in the shortest path from S to D, then we need to find the shortest distance between the missing color node and our shortest path from S to D.
- To achieve this task, we can apply Multisource Breadth-First Search from all the nodes coloured in the same colour as the missing ball. That means we need to store a map[color]->vector of nodes with colour as color.
- Now for every colour ball whose count came 0 in the shortest path, do Multisource Breadth-First Search from all nodes of that colour in the graph. Once Breadth-First Search reaches a node marked as visited (shortest path node), that means we get the minimum distance of the coloured ball from the shortest path. Also since we want to take minimum time, so we will keep only one coloured ball of each colour. Additional time = 2*distance of nearest coloured ball of missing colour +1(wait to gain a coloured ball).
Time Complexity
O(V + E) where V is the number of vertices and E is the number of edges.
The time complexity of Depth-First Search traversal and Multisource Breadth-First Search is O(V + E). Hence the time complexity is O(V + E).
Space Complexity
O(V), where V is the number of vertices in the given graph.
We are creating a boolean visited array of size V Hence space complexity is O(V).
Code Solution
(100% EXP penalty)
Minimum time
C++ (g++ 5.4)
Console
