Mobile Pattern Lock.

Moderate
0/80
Average time to solve is 30m
profile
Contributed by
5 upvotes
Asked in company
Apple

Problem statement

Mobile Pattern Lock is a graphical password method where users create patterns on a line connecting 3*3 grid. You are given two integers ‘M’ and ‘N’. Count a total number of valid mobile pattern locks which consist of at least ‘M’ keys and at most ‘N’ keys. In a valid pattern, all keys must be distinct. The order of keys used matters. If the line joining two consecutive keys passes through any other keys, the other keys must be previously selected in pattern.

Example :

We can treat the 3*3 grid as follows:-

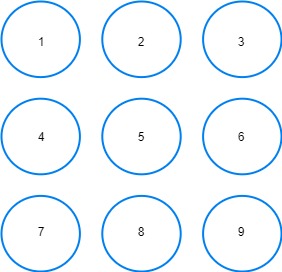
subsequence

4-7-9-6 is an invalid pattern lock because while joining 7-9 it passes through key 8 which has not been previously selected in pattern.
9-1-2-3 is an invalid pattern lock because while joining 9-1 it passes through key 5 which has not been previously selected in pattern.
4-2-6-8 is a valid pattern lock.

subsequence

Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains a single integer ‘T’ representing the number of test cases.

The only line of each test case contains two space-separated integers ‘M’ and ‘N’ representing two integers for which you need to return the total number of valid patterns.
Output Format : 
For each test case print an integer denoting the total number of valid mobile pattern locks which consist of at least ‘M’ keys and at most ‘N’ keys.
Note : 
You do not need to print anything; it has already been taken care of. Just implement the function.
Constraints : 
1 <= T <= 50
1 <= M <= N <= 9

Time Limit: 1sec
Sample Input 1 :
2
1 1
1 2
Sample Output 1 :
9
65

Explanation Of Sample Output 1 :

Test case 1:

1,2,3,4,5,6,7,8 and 9 are 9 possible patterns.

Test case 2:

Key with 1- 1,2,3,4,5,6,7,8 and 9 are 9 possible patterns.
Key with 2-  all adjacent pair, so total count is 56
Return 9+56.
Sample Input 2 :
2
2 2
4 6
Sample Output 2 :
56
34792
Hint

Try to iterate over all positions using DFS.

Approaches (1)
DFS

We can do DFS from all the starting points. We can easily observe 1,3,7, and 9 can be treated as the same i.e. the number of patterns for each one of them would be the same due to symmetry. Similarly, 2,4,6, and 8 will have the same number of patterns as a starting point. We can apply DFS as follows: 

 

  • We will declare an array/list vis which stores if the key was visited. Initially, all are initialized ‘false’.
  • To avoid invalid moves we will maintain a 2-D array ‘point[10][10]’ where ‘point[i][j]’ stores the index of the key in between line joining ‘i’ and ‘j’. If there are no points store it as 0.
  • Declare ‘ans’ and initialize it with zero.
  • Iterate over all path lengths from ‘m’ to ‘n’. For each length we will calculate as follows:-
    • We will write a recursive function  ‘int traverse(int currKey, int movesLeft, bool vis[10])’ where ‘currKey’ is key which we are at present and ‘movesLeft’ is the number of moves we are yet to make. We will implement the function as follows:-
      • If ‘movesLeft’ is zero we have come to the end of a valid pattern lock so we return 1.
      • We will mark ‘currKey’ visited i.e. ‘vis[currKey] = true’.
      • Declare ‘numberOfPaths’ and initialize it with zero.
      • We will iterate over all the keys. If ‘i-th’ key is not visited yet and either no key is present between ‘currKey’ and ‘i-th’ key or if the key is present it has already been visited. Then we can visit ‘i-th’ key next into our path. Therefore we call function recursively ‘numberOfPaths’ += ‘traverse(i, movesLeft-1, vis)’.
      • After iterating over all the keys mark ‘currKey’ as not visited i.e. ‘vis[currKey] = false’.
      • Return ‘numberOfPaths’.
    • We will now use the above recursive function:-
      • ‘ans’ += 4* ‘traverse(1, i-1, vis)’ , because 1,3,7, and 9 are similar.
      • ‘ans’ += 4* ‘traverse(2, i-1, vis)’ , because 2,4,6, and 8 are similar.
      • ‘ans’ += ‘traverse(5, i-1, vis)’.
  • Return ‘ans’
Time Complexity

O(N!), where ‘N’ is the maximum number of keys we can take in our path.

 

As we iterate over most of the pattern.

Space Complexity

O(K), where ‘K’ is the total number of keys.

 

As we are using an array ‘VIS’ of size ‘K’ to check which keys are visited already in the pattern.

Code Solution
(100% EXP penalty)
Mobile Pattern Lock.
Full screen
Console