Modify Matrix

Moderate

0/80

Average time to solve is 40m

Contributed by

2 upvotes

Asked in company

Problem statement

Given a square matrix in the form of a linked list with each node having the right and down pointer. Modify it in a singly linked list which should only be connected using the right pointer.

Detailed explanation ( Input/output format, Notes, Images )

Input format :

The first line contains an Integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.

The first line of each test case contains the size of the square matrix 'N'.

The second and final line of each test case contains the N*N Integers separated by a single space (the matrix is entered row-wise)

Output format :

For each test case, print the modified singly linked list which should only be connected using the right pointer.

Output for every test case will be printed in a separate line.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints :

1 <= 'T' <= 10
1 <= 'N'  <= 10^2
-10^9 <= data <= 10^9

Where 'N'  is the size of the square matrix.

Time Limit: 1sec

Sample Input 1 :

Sample Output 1 :

1 2 1 2 
1 2 2 1

Explanation For Sample Input 1 :

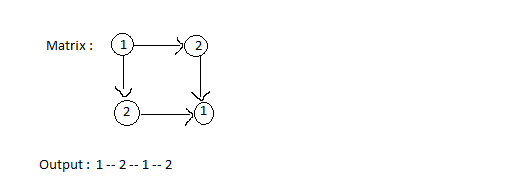
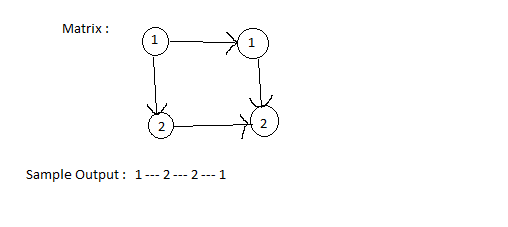
Sample Input 2:

2
2
3 4 2 4
3
1 2 3 4 5 6 7 8 9

Sample Output 2:

3 2 4 4 
1 4 7 8 9 2 5 6 3

Hint 1

Try to traverse in the given matrix from the extreme down then extreme right.

Approaches (1)

Approach 1

Modify Matrix

Starting from head of the linked list traverse first to the extreme bottom of the matrix and then go to the extreme right of the matrix. Update head to the right of the head and then again go from here to the second extreme bottom of matrix and then go to the second extreme right of the matrix and so on, update head to its right after every traversal, follow down and right path until ur head reaches null. Make shape of ‘L’ starting from the head of the linked list and update the head to its right node. With traversal of matrix, you have to change links from down to right in the updated linked list

Time Complexity

O(N^2), Where N is the size of the square matrix.

As every node is visited once and there are N^2 nodes in total. Hence the time complexity will be O(N^2).

Space Complexity

O(1)

As constant extra space is used.

(100% EXP penalty)

Modify Matrix

Console