Problem
Submissions
Hints & solutions
Discuss
Ninja and Binary Tree
Moderate
0/80
Average time to solve is 25m
2 upvotes
Asked in companies



Problem statement
Ninja has to implement a binary tree class from scratch. The Ninja can perform three types of queries on this binary tree.
- ‘I’ ‘VAL’: In this query, Ninja has to insert a Node with the value ‘VAL’ in the binary tree.
- ‘D’ ‘VAL’: In this query, Ninja has to delete a Node with the value ‘VAL’ from the binary tree.
- ‘R’: In this query, Ninja has to print a random node from the tree.
All the Node values in the binary tree are different. All nodes are equally likely to be chosen.
For example:
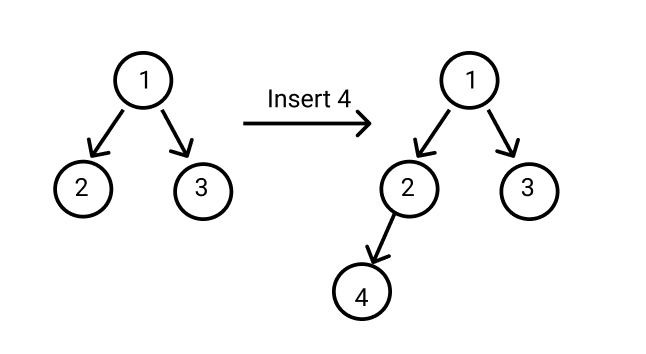
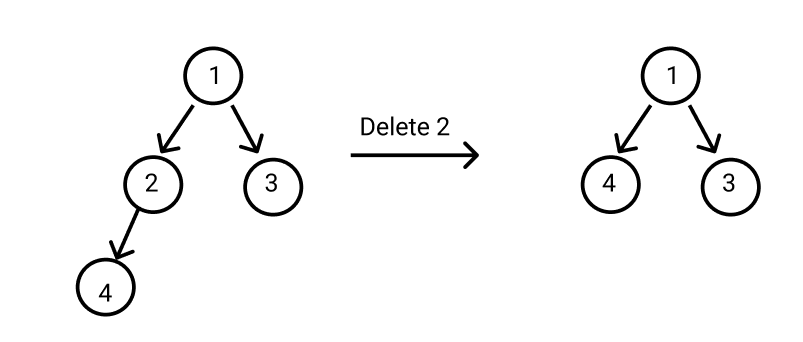
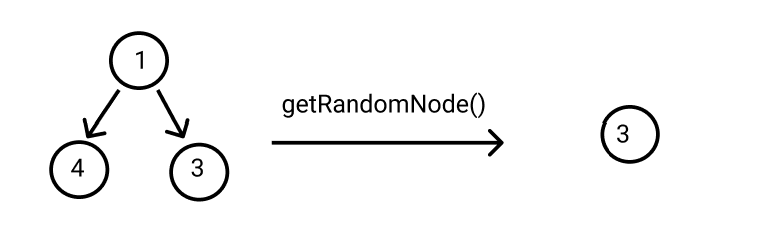
Detailed explanation ( Input/output format, Notes, Images )
Input Format
The first line of input contains an integer 'T' representing the number of test cases. Then the test cases follow.
The next line of each test case contains an integer ‘Q’ representing the number of queries to Ninja.
The next line, ‘Q’ lines of each test case, contain a character and integer representing which type of query is to perform on the binary tree and the value of the node.
For each test case, return the value of the Random Node obtained from the get Random Node query.
Print the output of each test case in a separate line.
Note:
You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints :
1 <= ‘T’ <= 10
1 <= ‘Q’ <= 10000
Char = {‘I’, ‘D’, ‘R’}
1 <= ‘VAL’ <= 100000
Time Limit: 1 second
Sample Input 1:
1
5
I 2
I 4
I 5
D 4
R
Sample Output 1:
Valid answer
Explanation for Sample Output 1:
For sample test case 1:
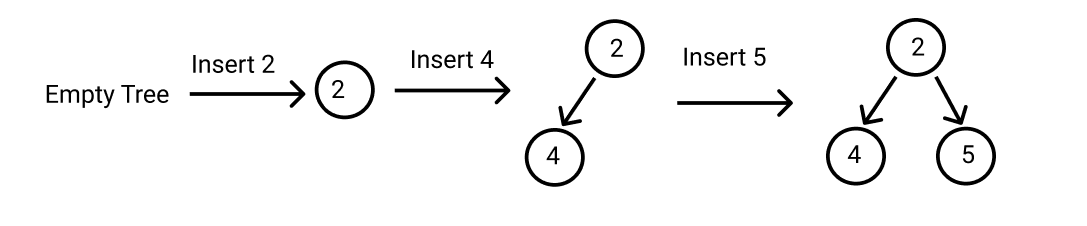
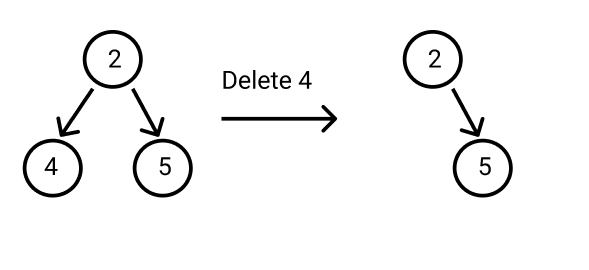
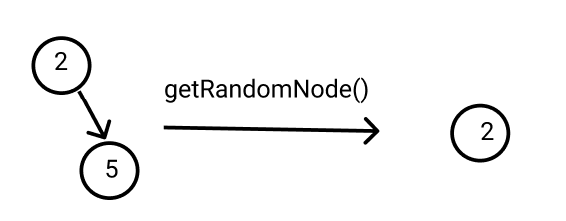
In this sample test case, the random nodes may be 2 or 5 because all nodes should be equally likely to be chosen. So you can print any one of them.
As the random node returned (here 2) exists in the tree, the output is a “Valid answer.
Sample Input 2:
1
5
I 4
I 2
D 2
I 5
R
Sample Output 2:
Valid answer
Explanation for Sample Output 2:
For sample test case 1:

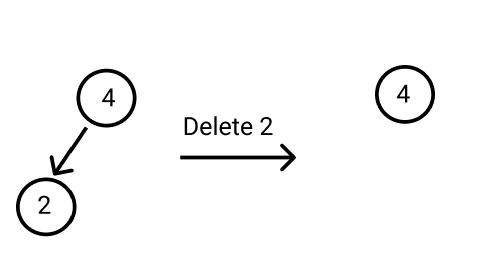
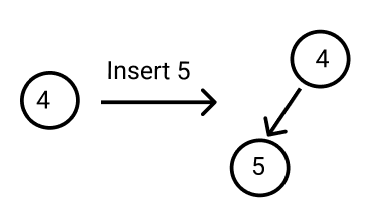

In this sample test case, the random nodes may be 4 or 5 because all nodes should be equally likely to be chosen. So you can print any one of them.
As the random node returned (here 4) exists in the tree, the output is a “Valid answer”.
Hint
Hint 1
Think of the brute force approach.
Approaches (1)
Approach 1
Brute Force
In this problem, we have to implement a binary tree class from scratch. We have to deal with 3 queries: Insert a node in the binary tree, Delete a node in the binary tree and get a random node in the binary tree. So we make three functions to deal with these three queries.
For inserting a node in the binary tree, first, we do iterative level order traversal in the given binary tree using a queue. If we find a node whose left/right child is empty, we make a new node with ‘VAL’ as the data of the node and add this node into the left/right child in the binary tree.
For deleting a node in the binary tree, first, we start from the root of the binary tree then find the deepest and rightmost node of the binary tree and the node which we want to delete. Then we replace the deepest rightmost node value with the node to be deleted. Then we delete the deepest right node.
For finding a random node in the binary tree, first, we store the inorder traversal of the binary tree in an array/list. Then we generate a random number between 0 to a number of nodes - 1 and return the value which is present at that random index in the array/list.
Here is the algorithm :
Insertion in the binary tree :
- If the root of the binary tree is null:
- Return a new node with the value ‘VAL’.
- We declare a queue in which we store nodes of the binary tree.
- Add the root of the binary tree in the queue.
- We run a loop while the queue is not empty:
- Remove the first element from the queue.
- If the left node of the current node is ‘NULL’ :
- Add a new node with the value ‘VAL’ to the left of the current node.
- Return root.
- If the right node of this node is ‘NULL’ :
- Add a new node with the value ‘VAL’ to the right of the current node.
- Return root.
- Add left and right nodes of the current node into the queue.
Deletion in the binary tree :
- If the root node is ‘NULL’:
- Return.
- If we are at the leaf node of the binary tree:
- Return.
- We declare a queue in which we store nodes of the binary tree.
- Add the root of the binary tree in the queue.
- We declare a node ‘NODE_TO_BE_DELETED’ and ‘DEEPEST_NODE’ in which we store a node that we have to delete and the rightmost deepest node in the binary tree.
- We run a loop while the queue is not empty:
- Remove the first element from the queue and store into ‘DEEPEST_NODE’
- If the ‘DEEPEST_NODE’ value is equal to ‘VAL’:
- ‘NODE_TO_BE_DELETED’ = ‘DEEPEST_NODE’
- If the left node of the ‘DEEPEST_NODE’ is not ‘NULL’:
- Add the left node of the ‘DEEPEST_NODE’ into the queue.
- If the right node of the ‘DEEPEST_NODE’ is not ‘NULL’:
- Add right node of the ‘DEEPEST_NODE’ into the queue
- If ‘NODE_TO_BE_DELETED’ is not ‘NULL’:
- ‘DEEPEST_NODE_VAL’ = ‘DEEPEST_NODE.DATA’
- DELETE_DEEPEST_NODE( ROOT,‘DEEPEST_NODE’).
- ‘NODE_TO_BE_DELETED.DATA’ = ‘DEEPEST_NODE_VAL’.
Function DELETE_DEEPEST_NODE( ROOT,‘DEEPEST_NODE’):
- We traverse on the binary tree using level order traversal.
- If the node of the binary tree is ‘DEEPEST_NODE’:
- Remove this node.
Get random node from the binary tree:
- We declare an array/list ‘ALL_NODES’ in which we store all nodes of the binary tree.
- We traverse on the binary tree and store all the nodes in ‘ALL_NODES’.
- We generate a random number between 0 to a number of nodes - 1.
- Return the value which is present at that random index.
Time Complexity
O(N) where ‘N’ represents the number of nodes in the binary tree.
For inserting a node in the binary tree we traverse all the nodes.
For deleting a node in the binary tree we traverse all the nodes.
For finding a random node in the binary tree first we traverse all the nodes and store into an array/list ‘allNodes’ and then print a random node. So the overall time complexity is
O(N).
Space Complexity
O(N) where ‘N’ represents the number of nodes in the binary tree.
For inserting a node in the binary tree we traverse all the nodes and store them into a queue.
For deleting a node in the binary tree we traverse all the nodes and stores them into a queue.
For finding a random node in the binary tree first we traverse all the nodes and store them into an array/list ‘ALL_NODES’ and then print a random node. So the overall space complexity is O(N).
Code Solution
(100% EXP penalty)
Ninja and Binary Tree
C++ (g++ 5.4)
Console
