Ninja And Bombs

Easy
0/40
Average time to solve is 15m
profile
Contributed by
8 upvotes
Asked in companies
FacebookAdrosonic

Problem statement

Ninja is on a secret mission and wants to reach the enemy's base camp. However, his enemies have planted bombs in a grid of ‘N’ rows and ‘M’ columns called ‘BOMB-GRID’. To reach the camp, Ninja has to safely cross ‘BOMB-GRID’. The value at each cell in ‘BOMB-GRID’ denotes the power of that bomb. An empty cell (without a bomb) is represented as 0. The ‘BOMB-GRID’ has the following properties:

1. If three or more bombs with the same power are adjacent vertically or horizontally, then they blast at the same time immediately and their cells become empty.

2. After the bombs blast simultaneously if an empty cell on ‘BOMB-GRID’ has a bomb on top of itself, then these bombs will drop until they hit a bomb or hit at the bottom at the same time. (No new bombs will drop from outside of the top boundary of the ‘BOMB-GRID').

3. After the above steps, there may exist more bombs that can be blasted. If so, the above steps will be repeated.

4. If there does not exist more bombs that can be blasted (ie. the 'BOMB-GRID' is safe), then return the current ‘BOMB-GRID’.

5. The time taken by bombs to shift from one position to another can be neglected.

We will call ‘BOMB-GRID' safe if and only if no more blasts happen in ‘BOMB-GRID’. Ninja wants to know the safe state of ‘BOMB-GRID’ after every possible blast.

As Ninja is busy planning, he asks you for help. Can you help Ninja determine the safe state of ‘BOMB-GRID’?

For Example : 
For the ‘BOMB-GRID’ shown below, the third grid represents a safe state i.e after all possible blasts.

img

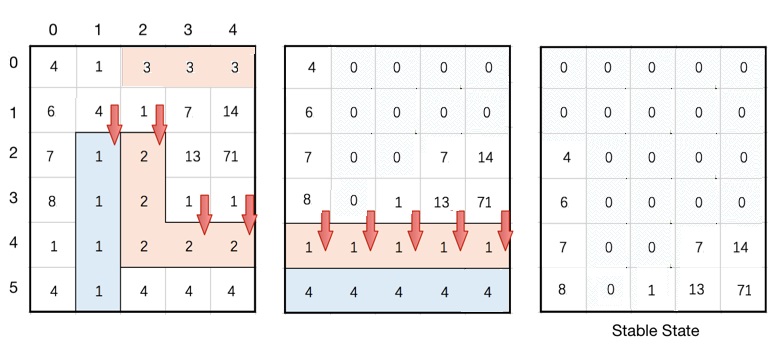
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line of input contains an integer ‘T’ denoting the number of test cases. Then each test case follows.

The first line of each test case contains two single space-separated integers ‘N’ and ‘M’ representing the number of rows and columns in ‘BOMB-GRID’, respectively.

The next ‘N’ lines of each test case contain ‘M’ single space-separated integers denoting the power of the bomb at each cell.
Output Format : 
For each test case, print the safe state of ‘BOMB-GRID’ in a row-wise manner.

Print the output of each test case in a separate line.
Note : 
You are not required to print the expected output; it has already been taken care of. Just implement the function.
Constraints : 
1 <= T <= 100
1 <= N <= 50
1 <= M <= 50
0 <= BOMB-GRID[i][j] <= 1000

Where BOMB-GRID[i][j] denotes the power of the bomb placed in the ‘i’-th row and ‘j’-th column of ‘BOMB-GRID’.

Time limit: 1 sec
Sample Input 1 :
2
4 3
1 0 1
2 0 4
2 1 1
1 2 3
3 3
1 1 1
1 2 1
1 1 1
Sample Output 1 :
1 0 1
2 0 4
2 1 1
1 2 3
0 0 0
0 0 0
0 2 0
Explanation For Sample Input 1 :
For the first test case :
The given ‘BOMB-GRID’ is safe as there exist no 3 or more than 3 bombs with the same powers adjacent together either horizontally or vertically.

For the second test case :
The given ‘BOMB-GRID’ all the bombs with power 1 in row 0, row 2 and column 0 and column 2 (0-based indexing) will blast simultaneously and the bomb with power 2 will be shifted to the bottom of column 1 as shown in the output. The ‘BOMB-GRID’ now becomes safe.
Sample Input 2 :
2
3 3
4 5 3
6 5 1
6 5 1
4 3
6 7 8
3 4 8
5 3 2
5 9 1
Sample Output 2 :
4 0 3 
6 0 1 
6 0 1 
6 7 8 
3 4 8 
5 3 2 
5 9 1
Hint

Try to use Brute Force with some optimizations

Approaches (1)
Brute Force Approach

The idea behind this approach is to pick all the bombs which are adjacent to 2 or more bombs horizontally or vertically and then blast them at the same time. After that, shift all the remaining bombs to the bottom-most bomb or at the bottom of ‘BOMB-GRID’ and replace the empty cells with 0s. Do this while we do not get a safe state of ‘BOMB-GRID’. 

 

Algorithm

 

Do the following while we do not get a safe state of ‘BOMB-GRID’:

 

  • Iterate through ‘BOMB-GRID’ and do the following:
    • Pick all the indices of bombs that are adjacent to 2 or more bombs with the same power horizontally or vertically and store them in an array/list ‘BLAST’.
  • Check if ‘BLAST’ is empty or not. The following two cases will arise:
    • If ‘BLAST’ is empty that means we are having the safe state of the ‘BOMB-GRID’. Simply return the ‘BOMB-GRID’.
    • Else iterate the ‘BOMB-GRID’ and for all the indices in the ‘BLAST’. Shift all the bombs which are vertically on top of these indices to the largest row containing non zero value of the ‘BOMB-GRID.
    • After shifting the bomb if the cell becomes empty we replace the cell value by 0 denoting an empty cell.
Time Complexity

O((N*M)^2) where ‘N’ and ‘M’ are the number of rows and the columns in the BOMB-GRID

 

Because in the worst-case, we have to iterate ‘BOMB-GRID’ after each blast and the maximum number of blasts can be ‘N*M’/3. So, the overall time complexity will be O((N * M)^2).

Space Complexity

O(1)

 

We are not using any extra space so space complexity will be O(1).

Code Solution
(100% EXP penalty)
Ninja And Bombs
Full screen
Console