Biconnected Components

Hard
0/120
Average time to solve is 70m
profile
Contributed by
5 upvotes
Asked in companies
FacebookJUSPAY

Problem statement

You are given an undirected graph of N nodes and M edges. You are required to find out the number of bi-connected components of the graph. We donot count an isolated vertex as a biconnected component

For Example:

alt text

Consider the following graph

4 4
1 3
1 2
2 3
3 4

The graph has two bi-connected components 

1 - 2, 2 - 3, 3 - 1

3 - 4

Hence the output is 2.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains a single integer ‘T’ denoting the number of test cases to be run. Then the test cases follow.

Each test case contains a line containing two integers ‘N’ and ‘M’. Then ‘M’ lines follow: 
Each line contains 2 space-separated integers ‘u’ and ‘v’ which means that there is an edge between ‘u’ and  ‘v’.
Output Format: 
For each test case, output a single line containing one integer - the number of bi-connected components in the graph.
Note: 
You are not required to print anything; it has already been taken care of. Just implement the function.
Constraints: 
1 <= T <= 10
1 <= N, M <= 10^4
1 <= u, v <= N

Time Limit: 1 sec.
Sample Input 1:
2
7 8
1 2
1 3 
1 4 
1 5
2 6
2 7
4 5 
7 6
3 2
1 2 
1 3
Sample Output 1:
4
2
Explanation For Sample Output 1:

link

In the above graph, the different biconnected components are:

2-7, 6-7, 2-6
1-3
1-2
1-4, 4-5, 4-5

link

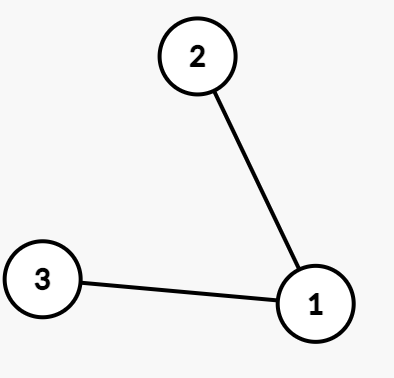
For test case 2 the graph looks as above. It has 2 biconnected components
1 - 2
1 - 3
Sample Input 2:
3
3 3
1 3
1 2
2 3
4 4
1 3
1 2
2 3
3 4
1 0
Sample Output 2:
1
2
0
Explanation For Sample Output 2:
In test case 3 since there is only 1 isolated vertex, we output 0.
Hint

Think similar to finding articulation points in the graph. Whenever an articulation point is found try to mark a new biconnected component.
 

Approaches (1)
Biconnected Components

Firstly you can read about bi-connected components here.

Since we need to make sure that our biconnected component should be connected and does not contain any articulation point, we maintain a stack of edges while performing DFS traversal of the graph and push the edges we traverse during the DFS into the stack. 

As we backtrack from the DFS traversal, say currently we are at edge v-to, we check if v is an articulation point i.e low[to] >= disc[v], if v is an articulation point then we pop the edges from the stack until the top of the stack is  ‘v-to’ and include ‘v-to’ too. The popped set of edges will form one biconnected component of the given graph.



 

Algorithm:


 

function biconnectedComponents(N, M, edges) takes the graph as input and returns the number of biconnected components in the graph.

  1. Call the dfs function for every unvisited node in the graph.
  2. Whenever a vertex is visited first time initialize the discovery time and the ‘low’ time of that vertex to the current time counter and increase it.
  3. For each vertex v in the adjacency list of u:
    1. if it is not visited, push the edge u - v in the stack and call the dfs for v.
      1. check if the subtree of v has a connection to one of the ancestors by updating low[u] = min(low[u], low[v]).
      2. If u is an articulation point, pop all the edges from the stack until this edge and increase the count of biconnected components by 1.
    2. If v is already visited, then update the low[u] time with the discovery time of v and push the edge into the stack.
  4. If the stack is not empty increase the number of components by 1.
  5. Finally, return the number of biconnected components in the graph.
Time Complexity

O(M + N), Where M is the number of edges and N is the number of vertices in the graph. 

 

We visit each vertex exactly once and each edge is pushed and popped exactly once from the stack.

Space Complexity

O(N + M), Where M is the number of edges and N is the number of vertices in the graph. 

We store the graph in the adjacency list format. Hence, the space complexity will be O(N + M).

Code Solution
(100% EXP penalty)
Biconnected Components
Full screen
Console