Number of Mismatching Bits

Easy
0/40
Average time to solve is 10m
9 upvotes
Asked in companies
Wells FargoCodenation

Problem statement

Given two integers "first" and "second". Find the number of bits that do not match in the binary representation of the given numbers.

For example, let "first" be 11 and "second" be 15. Writing both the given numbers in binary we get first = 1011(binary representation of 11) and second = 1111(binary representation of 15) we can see all the bits are the same except the second bit.

ex

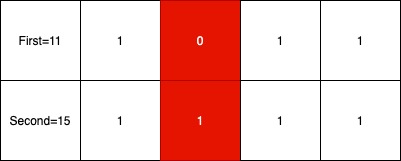
Therefore only 1 bit differs hence we return 1 as shown in the diagram.

Note: 
1. Do not print anything, just implement the provided function and return the number of mismatching bits for the given numbers.
Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line of input contains an integer ‘T’ denoting the number of test cases.
The next ‘T’ lines represent the ‘T’ test cases.
The only line of each test case contains 2 space-separated integers "first" and "second"
Output Format 
For each test case, print a single integer denoting the number of mismatched bits in their binary representation.

The output of each test case will be printed in a separate line.
Constraints: 
1 <= T <= 10 ^ 5
0 <= first, second <= 10^9

Where ‘T’ is the total number of test cases and "first", " second" are the given numbers.

Time limit: 1 second
Sample Input 1:
2
11 15
12 16
Sample Output 1:
1
3
Explanation of sample input 1 :
Test Case 1:

We get "first" is equal to 11 and "second" is equal to 15.

Converting to binary representation, we get 
First = 11 = 2^3 + 2^1 + 2^0
First = 1011
Second = 15 = 2^3 + 2^2 + 2^1 + 2^0
Second = 1111

ex

We can see that the first third and fourth bits are the same in both the numbers but the second bit is different,  it is 0 in the first number and 1 in the second number. Since only 1 bit differs, we return 1.

Test Case 2: 

We get "first" = 12 and "second" = 16.

Converting to binary, we get 
First = 12 = 2^3 + 2^2
First = 01100
Second = 16 = 2^4
Second = 10000

alt-2

We can clearly see that the first second and third bit differ(highlighted in red) therefore we return 3.
Sample Input 2:
4
100 1000
5 13
6 20
21 23
Sample Output 2:
5
1
2
1
Hint

Check if every bit is same or not

Approaches (2)
Brute force Approach

The key idea is to check for each bit if it is different or not.

Consider the following steps:

  1. Create a variable “count” which stores the count of mismatched bits. Initialize it to zero.
  2. Create a loop using a variable ‘i’ such that 0 <= ‘i’ < 30 since 2^30 > 10^9
    1. Right shift the “first” and “second” ‘i’ times and check if the last bit is matching or not. We can easily do this by taking AND with 1 and then comparing.
    2. If it doesn't match then increment the “count” by 1.
  3. Return the “count”.
Time Complexity

O(1)

 

In each case, we perform 30 operations which is a constant hence it takes constant time.

Space Complexity

O(1). 

 

We are using constant space

Code Solution
(100% EXP penalty)
Number of Mismatching Bits
Full screen
Console