Problem
Submissions
Hints & solutions
Discuss
Number of operations to make Graph connected.
Easy
0/40
Average time to solve is 15m
14 upvotes
Asked in companies



Problem statement
You have been given a graph consisting of ‘N’ vertices numbered from 1 to ‘N’. The graph has ‘M’ edges. In an operation, you can shift an edge between two directly connected vertices to between pair of disconnected vertices to make them directly connected. Return the minimum number of operations to make the graph connected. If it is not possible to make graph connected return -1.
Example:Let’s say ‘N’ is 4 and ‘M' is 3. The 3 edges are (1,2), (2,3) and (1,3). Then our graph will look as follows:-
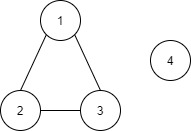
To make the graph connected we can shift the edge between (1,3) to (1,4). This operation will make the graph connected. There are multiple ways in which we can make graph connected. So, in this case, we can make graph connected in just one operation.
1. A connected graph is a graph that is connected in the sense of a topological space, i.e., there is a path from any vertex to any other vertex in the graph.
2. There are no repeated edges and self-loops in the graph.
3. You do not need to print anything; it has already been taken care of. Just implement the function.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line contains a single integer ‘T’ representing the number of test cases.
The first line of each test case contains two space-separated integers ‘N’ and ‘M’ representing the number of vertices and the number of edges in the graph.
Each of the next ‘M’ lines contains two space-separated integers representing the vertices that are directly connected by an edge.
For each test case, print a single line containing a single integer denoting the minimum number of operations to make the graph connected. If it is not possible to make graph connected return -1.
The output of each test case will be printed in a separate line.
Note:
You do not need to input or print anything, as it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 10
1 <= N <= 10000
1 <= M <= 10000
1 <= U[i], V[i] <= N
Where ‘T’ is the number of test cases.‘N’ is the number of vertices in the graph. ‘M’ is the number of edges in the graph. ‘U[i]’ and ‘V[i]’ are vertices of the i-th edge.
Time Limit: 1sec.
Sample Input 1:
2
4 3
1 2
2 3
3 1
4 3
1 2
2 3
3 4
Sample Output 1:
1
0
Sample Output 1 Explanation:
Test case 1:
The graph looks as follows:-

Initially, graph is disconnected. We can apply one operation and shift the edge between (2,3) to (3,4). This operation will make the graph connected. The graph after the operation will look as follows:-

Therefore the answer is 1.
Test case 2:
The graph looks as follows:-

The graph is already connected so we don’t need to make any operation.
Therefore the answer is 0.
Sample Input 2:
2
4 2
1 2
3 4
4 6
1 2
1 3
1 4
2 3
2 4
3 4
Sample Output 2:
-1
0
Hint
Hint 1
Hint 2
Find the number of connected components.
Approaches (2)
Approach 1
Approach 2
Breadth First Search.
For a graph with ‘N’ vertices to be connected, there must be at least ‘N’ - 1 edges in the graph. If a graph has less than ‘N' - 1 edges it is impossible to make the graph connected. Otherwise, it is always possible to make graph connected. As we need to find the minimum number of operations to make the graph connected we will think greedily. We will find the total number of connected components in the graph. We can treat each connected component in the graph as a single vertex. Basically, we want to shift edges such that these components become connected. Therefore answer will be the total number of connected components - 1.
We will apply the algorithm as follows:-
- If ‘m’ is less than ‘N’ - 1 return -1.
- Declare a list of list/vector ‘adj’ of size ‘N’ + 1 where ‘adj[i]’ stores vertices that are directly connected to node ‘i’.
- Iterate ‘i’ from ‘1’ to ‘m’:-
- Therefore push ‘v[i]’ in ‘adj[u[i]]’ and ‘u[i]’ in ‘adj[v[i]]’.
- Maintain an auxiliary array ‘vis’ which maintains if ‘i-th’ vertex has been visited.
- Declare ‘ctr’ and initialize it with ‘0’. It stores the number of connected components.
- Iterate ‘i’ from ‘1’ to ‘N’:-
- If node ‘i’ has not been visited yet:-
- Mark node ‘i’ as visited and insert it in the queue.
- Increase ‘ctr’ by ‘1’ as it is a new component.
- Iterate till the queue is empty:-
- Pop the front element of ‘q’ and store it in ‘u’.
- Iterate over ‘adj[u]’
- If the ‘adjacentNode’ is not visited yet. Mark ‘vis[adjacentNode]’ as true and insert ‘adjacentNode’ in queue.
- If node ‘i’ has not been visited yet:-
- Declare ‘ans’ and initialize it with ‘ctr’ - 1.
- Return ‘ans’.
Time Complexity
O(N + M), where N denotes the number of vertices and M denotes the number of edges in the graph.
We are visiting each vertex and edge once.
Space Complexity
O(N + M), where N denotes the number of vertices and N denotes the number of edges in the graph.
We build an adjacency list where ‘i-th’ vector/list can be of size N.
Code Solution
(100% EXP penalty)
Number of operations to make Graph connected.
C++ (g++ 5.4)
Console
