Number Of Triangles In Directed And Undirected Graphs

Moderate
0/80
Average time to solve is 30m
profile
Contributed by
12 upvotes
Asked in companies
LinkedInIBMOptum

Problem statement

Ninja has been given two Graphs: a directed graph ‘DIRGRAPH’ and an undirected graph ‘UNDIRGRAPH’. Ninja has to count the number of triangles in each of the graphs.

Can you help Ninja with finding the number of triangles in ‘DIRGRAPH’ and ‘UNDIRGRAPH’.

For Example :

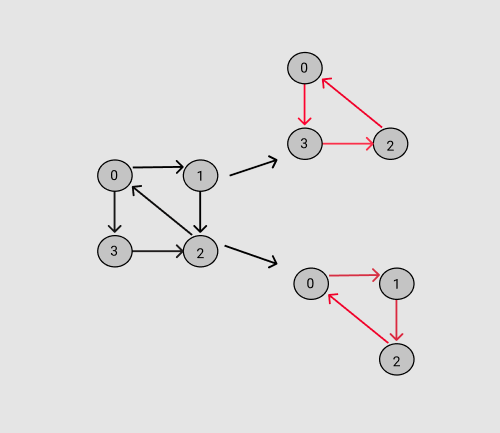
graph1

In this example, this graph is directed and there are two triangles possible.
Triangle 1 : (0 3 2)
Triangle 2 : (0 1 2)

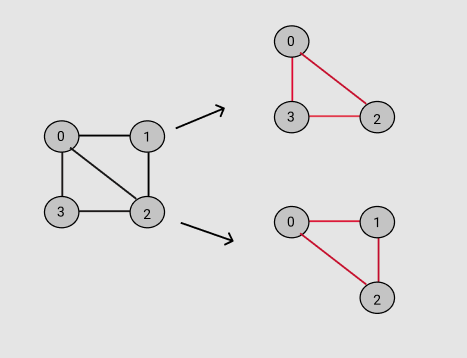
graph1

In this example, this graph is undirected and there are two triangles possible.
Triangle 1 : (0 3 2)
Triangle 2 : (0 1 2)
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line of input contains an integer ‘T’ which denotes the number of test cases or queries to be run. Then the test cases follow.

The first line of each test case contains two space-separated integers ‘V1’ and ‘E1’, which represents the number of vertices present in ‘DIR_GRAPH’ and the number of edges present in  ‘DIR_GRAPH’.

The next ‘E1’ lines of each test case contain two single space-separated integers, that denote that there exists an edge between vertex a1 and b1.

The next lines of each test case contain two space-separated integers ‘V2’ and ‘E2’, which represent the number of vertices present in ‘UNDIR_GRAPH’ and the number of edges present in  ‘UNDIR_GRAPH’.

The next ‘E2’ lines of each test case contain two single space-separated integers, that denote that there exists an edge between vertex a2 and b2.
Output Format : 
For each test case, print the number of triangles in ‘DIR_GRAPH’ and ‘UNDIR_GRAPH’.

Print the output of each test case in a separate line.

Note :

You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints : 
1 <= ‘T’ <= 100
2 <= ‘V1’,’V2’ <= 1000
1 <= ’E1’ <=  (V1 * (V1 - 1)) / 2
1 <= ’E2’ <=  (V2 * (V2 - 1)) / 2
0 <= ‘a1’, ‘b1’ <= ‘V1’ - 1
0 <= ‘a2’, ‘b2’ <= ‘V2’ - 1

Time Limit: 1 sec

Sample Input 1 :

1
4 5
0 1 
1 2
2 0
0 3
3 2
4 5
0 1 
1 2
2 0
0 3
3 2
Sample Output 1 :
2 2

Explanation Of Sample Output 1 :

For sample test case 1 :

graph1

For a directed graph, there are two triangles possible.
Triangle 1 : (0 3 2)
Triangle 2 : (0 1 2)

graph1

For an undirected graph, there are two triangles possible.
Triangle 1 : (0 3 2)
Triangle 2 : (0 1 2)

Sample Input 2 :

1
5 7
0 3 
3 2
3 4
2 4
2 0
1 0
1 2
5 7
0 3 
3 2
3 4
2 4
2 0
1 0
1 2
Sample Output 2 :
1 3

Explanation Of Sample Output 2 :

For sample test case 1 :

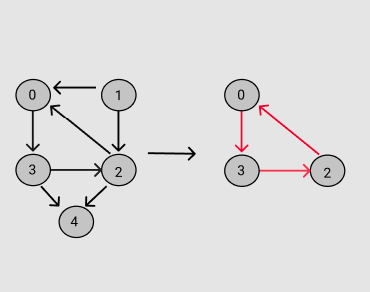
graph1

For a directed graph, there is only one triangle possible.
Triangle 1 : (0 3 2)

graph1

For an undirected graph, there are three triangles possible.
Triangle 1 : (0 3 2)
Triangle 2 : (0 1 2)
Triangle 3 : (2 3 4)
Hint

Think of Brute Force Approach.

Approaches (1)
Brute Force

First, we run three nested loops to find all the triplets ‘VER1’, ‘VER2’, and ‘VER3’ where VER1’, ‘VER2’, and ‘VER3’ represents our first, second, and third vertices of the given graph.

The ‘UNDIR_GRAPH’ triplets ‘VER1’, ‘VER2’, and ‘VER3’ can be permuted to give six combinations. So we divide the total ‘COUNT_TRIANGLE_In_UNDIR_GRAPH’ by 6 to get the actual numbers of triangles.

 

 For example : 

 If ‘VER1’ = 1

 ‘VER2’ = 2

 ‘VER3’ = 3.

Then all possible permutations are { (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1),(3, 1, 2), (3, 2, 1) }.

 

The ‘DIR_GRAPH’ triplets ‘VER1’, ‘VER2’, and ‘VER3’ can be permuted to give three combinations because, in a directed graph, the order of vertices is essential. So we divide the total ‘COUNT_TRIANGLE_In_DIR_GRAPH’ by 3 to get the actual numbers of triangles.

 

 For example: 

 If ‘VER1’ = 1

 ‘VER2’ = 2

 ‘VER3’ = 3.

Then all possible permutations are { (1, 2, 3), (2, 3, 1), (3, 1, 2) }

 

 

Algorithm:

  1. We declare two variables ‘COUNT_TRIANGLE_In_DIR_GRAPH’ and ‘COUNT_TRIANGLE_In_UNDIR_GRAPH’ in which we store the number of triangles in ‘DIR_GRAPH’ and ‘UNDIR_GRAPH’ respectively.
  2. We make an adjacency 2-D matrix ‘ADJ_MAT_DIR_GRAPH’ for ‘DIR_GRAPH’.
  3. We make an adjacency 2-D matrix  ‘ADJ_MAT_UNDIR_GRAPH’  for ‘UNDIR_GRAPH’.
  4. We run a loop for ‘i’ = 0 to ‘V1’
    • We run a loop for ‘j’ = 0 to ‘V1’
      • We run a loop ‘k’ = 0 to ‘V1’
      • If ADJ_MAT_DIR_GRAPH[i][j] == 1 and ADJ_MAT_DIR_GRAPH[j][k] == 1 and ADJ_MAT_DIR_GRAPH[k][i] == 1
        • ‘COUNT_TRIANGLE_In_DIR_GRAPH’++.
  5. We run a loop for ‘i’ = 0 to ‘V2’
    • We run a loop for ‘j’ = 0 to ‘V2’
      • We run a loop ‘k’ = 0 to ‘V2’
      • If ADJ_MAT_UNDIR_GRAPH[i][j] == 1 and ADJ_MAT_UNDIR_GRAPH[j][k] == 1 and ADJ_MAT_UNDIR_GRAPH[k][i] == 1
        • ‘COUNT_TRIANGLE_In_UNDIR_GRAPH’++.
  6. Finally, return ‘COUNT_TRIANGLE_In_DIR_GRAPH’ / 3  and ‘COUNT_TRIANGLE_In_UNDIR_GRAPH’ / 6.
Time Complexity

O(max(V1, V2) ^ 3)  Where ‘V1’ and ‘V2’ are the numbers of vertices of ‘DIR_GRAPH’ and ‘UNDIR_GRAPH’.

 

Because we are using three nested loops. So the overall complexity is O(max(V1, V2) ^ 3).

Space Complexity

O(max(V1, V2) ^ 2). Where ‘V1’ and ‘V2’ are the numbers of vertices of ‘DIR_GRAPH’ and ‘UNDIR_GRAPH’.

 

Because we are creating an adjacency matrix for both graphs. So space complexity will be O(max(V1, V2) ^ 2).

Code Solution
(100% EXP penalty)
Number Of Triangles In Directed And Undirected Graphs
Full screen
Console