Gray Code

Moderate
0/80
Average time to solve is 25m
profile
Contributed by
9 upvotes
Asked in companies
QuikrIBMIBM

Problem statement

Given a number ‘grayNumber’. Find the gray code sequence.

Conditions for a gray code sequence :

1. Gray code sequence contains numbers from 0 to 2^'grayNumber'-1 in bit/binary form.
2. Two consecutive gray code sequence numbers only differ by 1 bit.
3. Gray code sequence must start with 0.

Example :

Given 'grayNumber' : 2.

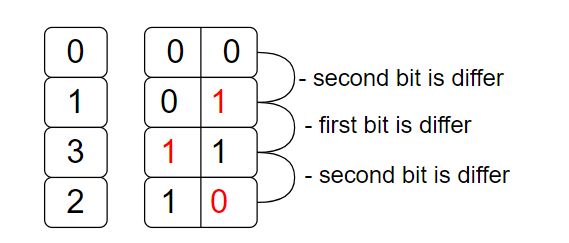
alt text

As depicted from above image, the gray code sequence is 0,1,3,2.

Note :

1. The output sequence must contain the decimal representation of numbers instead of the binary form.
2. There can be multiple answers print anyone.
Detailed explanation ( Input/output format, Notes, Images )
Input format : 
The first line of input contains an integer ‘T’ denoting the number of test cases.

The first line of every test case contains an integer ‘grayNumber’.
Output Format : 
For each test case, return the ‘list/vector’ of the Gray code sequence.

The output is ‘Valid’ if returned gray code sequence is correct. Else ‘Invalid’.
Note : 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints : 
1 <= T <= 2
0 <= grayNumber <= 15

Time Limit : 1 sec
Sample Input 1 :
2
2
3
Sample Output 1 :
Valid 
Valid
Explanation For Sample Input 1 :
For first test case,
Given 'grayNumber' :  2
Bits representation of a number from 0 to 2^2-1 = 3 is “ 00, 01, 10, 11’’.
But we have arranged these bits in such a way that two consecutive bits only differ by 1.
Only one possible way is “00, 01, 11, 10 ”.
Hence return value of every number “ 00 - 0 , 01 - 1, 11 - 3, 10 - 2”.
Sequence : {0, 1, 3, 2}.

For second test case,
Given 'grayNumber' : 3
Bits representation of a number from 0 to 2^3-1 =7 is “000, 001, 010, 011, 100, 101, 110, 111’’.
But we have arranged these bits in such a way that two consecutive bits only differ by 1.
One of the possible ways is “000, 001, 011, 111, 101, 100, 110, 010”.
Hence return value of every number “000 - 0, 001 - 1, 011 - 3, 111 - 7, 101 - 5, 100 - 4, 110 - 6, 010 - 2 ”.
Sequence : {0, 1, 3, 7, 5, 4, 6, 2}.

One another possible sequence can be : {0, 1, 3, 2, 6, 7, 5, 4}.
Sample Input 2 :
2
4
1
Sample Output 2 :
Valid 
Valid
Explanation For Sample Input 2 :
For first test case,
Given 'grayNumber' : 4
Sequence : {0, 1, 3, 2, 6, 7, 5, 4, 12, 13, 15, 14, 10, 11, 9, 8}.

For second test case,
Given 'grayNumber' : 1
Sequence : {0, 1}.
Hint

Observe the pattern of the Gray code sequence.

Approaches (4)
Iterative

Suppose are finding an answer for ‘N’ size but we have already the solution for ‘N-1’. then use the previous answer for a new answer. (where ‘N’ is ‘grayNumber’)

 

  1. Let’s consider ‘N' : 3 and we have solution of ‘N-1' : 2 : { ‘00’, ‘01’, ‘10’, ‘11’} and called it ‘PRE’.
  2. Create a new list/vector of ‘PRE’ in reverse order { ‘11’, ‘10’, ‘01’, ‘00’ } called it ‘NEW’.
  3. Add ‘0’ as a prefix, in all the elements of ‘PRE’ : { ‘000’, ‘001’, ‘010’, ‘011’ } /
  4. Add ‘1’ as a prefix, in all the elements of ‘NEW’ : { ‘111’, ‘110’, ‘101’, ‘100’} .
  5. Concatenate the ‘PRE’ + ‘NEW’ and it will be answered for ‘N' : 3.
  6. Return a number conversion of new concatenated ‘list/vector’.
Time Complexity

O(2^N*Log(N)), where ‘N’ is the given number ‘grayNumber’.

 

We are iterating the loop of size ‘2^N and Log(n) represents the number of bits in number ‘N’ in binary bits representation. Therefore, the overall time complexity will be O(2^N*Log(N)).

Space Complexity

O(2^N), where 'N' is the given number 'grayNumber'.

 

We are using a list/vector ('grayCode') of size 2^'N' to store the numbers. Therefore, the overall space complexity will be O(2^N).

Code Solution
(100% EXP penalty)
Gray Code
Full screen
Console