Optimal BST

Hard
0/120
Average time to solve is 55m
39 upvotes
Asked in companies
OracleShareChatLinkedIn

Problem statement

Given a sorted array of keys of BST and an array of frequency counts of each key in the same order as in the given inorder traversal. The frequency of an element is the number of searches made to that element. Construct a binary search tree from the given keys such that the total cost of all the searches is minimum.

Cost of searching a key is its frequency multiplied by its level number in the BST.

A binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree whose internal nodes each store a key greater than all the keys in the node's left subtree and less than those in its right subtree.

For example:

Input keys = [ 1, 3, 5 ] 
Frequency = [ 3, 10, 7 ] 

All the unique BST possible from the given keys are: 


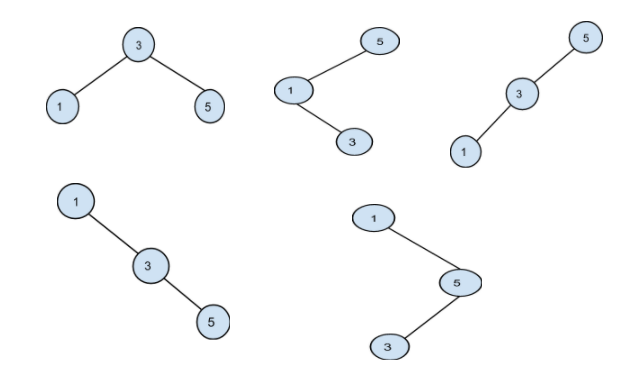
Among all these possible BST, the minimum cost is obtained from the below BST: 


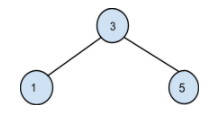
Cost = 1 * (freq of 3) + 2 * (freq of 1) + 2 * (freq of 5) = 30 
where 1 is the level of node 3, 2 is the level of the node 1 and node 5.
Detailed explanation ( Input/output format, Notes, Images )
Input Format 
The first line of input contains an integer T, the number of test cases.
The first line of each test case contains an element ‘N’ denoting the number of elements in the BST. 
The second line of each test case contains ‘N’ space separated integers, sorted in ascending order. 
The third line of each test case contains ‘N’ space separated integers denoting the frequency of each element of the BST.
Output Format: 
For every test case, print the minimum total cost of constructing the BST. 
The output of each test case is printed in a separate line.
Note 
1. Given BST will not contain duplicates. 
2. You don’t have to print anything, it has already been taken care of. Just implement the function.
Constraints: 
1 <= T <= 5
2 <= N <= 50
0 <= data <= 10^4

Where ‘T’ is the number of test cases, ‘N’ is the number of nodes in the given tree and ‘data’ denotes the value of the nodes in the given tree.
Sample Input 1:
1
3
1 3 5 
3 10 7
Sample Output 1:
30
Explanation of sample input 1:
All the possible BST’s for the given input are shown in the above example.

Searching cost in first BST = 1 * 10 + 2 * 3 + 2 * 7 = 30. 
Searching cost in second BST = 1 * 7 + 2 * 3 + 3 * 10 = 43. 
Searching cost in third BST = 1 * 7 + 2 * 10 + 3 * 3 = 36.
Searching cost in fourth BST = 1 * 3 + 2 * 10 + 3 * 7 = 44. 
Searching cost in fifth BST = 1 * 3 + 2 * 7 + 3 * 10 = 47. 

Thus, 30 is the minimum cost of all the searches.
Sample Input 2:
1
3
1 2 3
25 10 20
Sample Output 2
95
Hint

Can you solve this using recursion?

Approaches (4)
Recursion

This problem can be solved by solving its subproblems and then combining the solutions of the solved subproblems to solve the original problem. We will do this using recursion.

The idea is very simple. We will consider each key as the root and find an optimal solution by recursively finding the cost of left and right subtree. Then we will add the cost of the left and right subtree to the current’s node cost. 

Cost of a node is the product of its frequency and its level.  
 

Algorithm: 

  • Create a helper function ‘optimalCostHelper’ to find the minimum cost to construct a bst.
  • Call this helper function by passing the keys, frequencies, starting and the ending index of the keys in consideration, and level/depth of the current root.

Algorithm for optimalCostHelper(keys, frequencies, startIdx, endIdx, curLevel):

  • If we have checked for all the nodes, return 0.
  • Initialise an integer variable ‘minimumCost’ by the maximum positive value.
  • Run a loop from startIdx to endIdx:
    • Consider the current node as the root node.
    • Recursively find the optimal cost of left and right subtree. The level of a child node is 1 + the level of the parent node i.e 1 + curLevel.
    • Now, current’s node cost is the sum of product of its frequency and level, optimal cost for left subtree and optimal cost for right subtree.
    • If this cost is less than the ‘minimumCost’, update ‘minimumCost’.
  • Return the minimum cost to construct the binary search tree.
Time Complexity

O(3 ^ N), where N is the number of keys. 

We are considering every key as the root of the BST and then calculating the searching cost. In the worst case, we will be exploring all the possible BST’s that can be constructed from the given keys. With ‘N’ keys we can construct (2 * N) ! / (( N + 1 ) ! * (N!)) unique BST’s. This can be further generalized and the final time complexity will become O(3 ^ N).

Space Complexity

O(N), where N is the number of keys. 

Recursion stack space of O(N) is used. 

Video Solution
Unlock at level 3
(75% EXP penalty)
Code Solution
(100% EXP penalty)
Optimal BST
Full screen
Console