Pascal's Triangle

Easy
0/40
Average time to solve is 20m
381 upvotes
Asked in companies
IBMGrabInca Infotech Technologies Private Limited

Problem statement

You are given an integer N. Your task is to return a 2-D ArrayList containing the pascal’s triangle till the row N.

A Pascal's triangle is a triangular array constructed by summing adjacent elements in preceding rows. Pascal's triangle contains the values of the binomial coefficient. For example in the figure below.

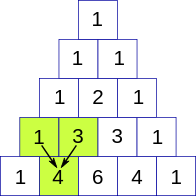
For example, given integer N= 4 then you have to print.

1  
1 1 
1 2 1 
1 3 3 1

Here for the third row, you will see that the second element is the summation of the above two-row elements i.e. 2=1+1, and similarly for row three 3 = 1+2 and 3 = 1+2.
Detailed explanation ( Input/output format, Notes, Images )
Input format : 
The first line of input contains an integer ‘T’ denoting the number of test cases.
The first line of each test case contains a single integer N denoting the row till which you have to print the pascal’s triangle.
Output format : 
For each test case, return the 2-D array/list containing the pascal’s triangle till the row N.
Note: 
You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 40
1 <= N <= 50

Time Limit: 1 sec
Sample Input 1 :
3
1
2
3
Sample Output 1 :
1
1 
1 1 
1 
1 1 
1 2 1
Explanation of The Sample Input 1:
For the first test case:
The given integer N = 1 you have to print the triangle till row 1 so you just have to output 1.

For the second test case:
The given integer N = 2 you have to print the triangle till row 2 so you have to output 
1
1 1

For the third test case
The given integer N = 3 you have to print the triangle till row 3 so you have to output 
1
1 1
1 2 1
Sample Input 2 :
3
4
5
6
Sample Output 2 :
1 
1 1 
1 2 1
1 3 3 1 
1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1
1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1
1 5 10 10 5 1
Hint

Try to think about how you get the values of coefficients recursively.

Approaches (3)
Recursive Solution

The idea is to use recursion to get the value of the coefficients we will create a helper function CALPASCAL which will take row and entry as its input parameters and we call this function in the main function of PRINTPASCAL.

  • Inside the function CALPASCAL if the row is 0 or the entry is equal to row then we will just return 1.
  • Else we will return the sum of adjacent previous row value that is CALPASCAL(I-1,J-1) + CALPASCAL(I-1,J).
  • Now for the main function to store the pascal’s triangle PRINTPASCAL inside this declare a 2-D arrayList TRIANGLE  and run loop from row I=0 to I<N.
  • Inside this loop run a loop from entry J=0 till entry J=R.
  • Inside this loop calculate the answer for each entry by calling the CALPASCAL function and add it to the arraylist.
  • Finally return the arraylist.
Time Complexity

O(2^N), Where ‘N’ denotes the number of Rows.

 

As we are calculating the coefficients every time in the row and the sum of coefficients for each row is 2^R where R is the row number and for all rows, it will give 2^N (by applying geometric progression).

Space Complexity

O(N), Where ‘N’ denotes the number of Rows.

 

We need O(N) space to store all the values of a given row in a list. Also at worst case, our recursion will need O(N) stack space for the recursive call.

Code Solution
(100% EXP penalty)
Pascal's Triangle
Full screen
Console