Find if Path Exists in Graph

Easy
0/40
Average time to solve is 45m
profile
Contributed by
1 upvote
Asked in company
MagicPIN

Problem statement

You are given an undirected graph consisting of ‘N’ nodes from 0 to ‘N’ - 1. You are given a list ‘EDGES’ of size ‘M’, consisting of all the edges of this undirected graph, and two nodes ‘SOURCE’ and ‘DESTINATION’ of this graph. Determine whether there exists a path from node ‘SOURCE’ to node ‘DESTINATION’. In other words, check whether there exists a path from node ‘SOURCE’ to node ‘DESTINATION’ by moving along the edges of the graph.

Note: 
The graph has no self-edges, no parallel edges.
The graph may not be connected.
For Example, 
If ‘N’ = 7, ‘M’ = 5, ‘SOURCE’ = 1, ‘DESTINATION’ = 5, EDGES = [ [2, 4], [2, 5],[3, 5],[3, 6],[4, 5] ].


Here, you can see that the graph is not connected and there is no way we can reach node 5 from node 1 as they both are in different connected components. Hence, the output is “No”.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line of input contains an integer ‘T’ denoting the number of test cases. then ‘T’ test cases follow.

The first line of each test case consists of four space-separated integers  ‘N’, ‘M’, ‘SOURCE’, ‘DESTINATION’, described in the problem statement.

Then next ‘M’ lines follow in each test case. The ith line consists of two space-separated integers ‘EDGES[i][0]’ and ‘EDGES[i][1]’ representing that there is a undirected edge between nodes ‘EDGES[i][0]’ and ‘EDGES[i][1]’.
Output Format : 
For each test case, print the “Yes” if there exists a path from node ‘SOURCE’ to node ‘DESTINATION’ by moving along the edges of the graph, Otherwise, print “No”.

Print a separate line for each test case.
Note : 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 10
1 <= N <= 500
1 <= M <= (N*(N-1)) / 2
0 <= ‘SOURCE’, ‘DESTINATION’ <= N - 1
Time limit: 1 sec
Sample Input 1 :
2
7 5 1 5
2 5
2 4
3 5
3 6
4 5
7 7 1 6
0 1
1 5
2 5
2 3
5 3
5 4
6 3
Sample output 1 :
 No
 Yes
Explanation For Sample Output 1:
For the first test case, the graph will be:


Here, you can see that the graph is not connected and there is no way such that we can reach node 5 from node 1 as they both are in different connected components. Hence, the output is “No”.

For the second test case, the graph will be:


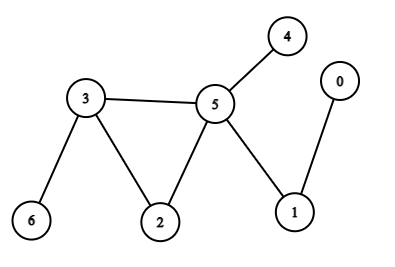
Here, source = 1 , destination = 6, We can reach node 6 from node 1 as 1 -> 5 -> 3 ->6.
Hence, the output is “Yes”.
Sample Input 2 :
2
6 8 5 1
0 4
0 5
1 2
1 5
3 5
3 4
4 2
5 2
10 14 4 8
0 2
1 8
1 0
2 6
3 1
3 7
4 7
5 7
5 6
6 7
8 2
8 0
9 2
9 6
Sample output 2 :
Yes
Yes
Hint

Can you make a recursive function that traverses the different paths in the graph?

Approaches (2)
Recursive Approach (Dfs)

Let’s first define a function canReach(node, x, adj, vis) where “node” is the current node we are at, ‘x’ is the destination node which we have to find, “adj” is the adjacency list of all the nodes, adjacency list stores all the nodes which are directly connected to the ith node, “vis” is the vector which keeps track of every node whether it has been traversed or not. If vis[node] = 1, means we have traversed this node, otherwise not.

 

This function returns “true” if ‘x’ is found otherwise it returns false. So, the idea is to start from the source node and try to find ‘x’ over all possible paths. After reaching a certain node we will check whether this node is equal to the ‘x’ or not, if yes then return “true”, otherwise traverse the adjacency list of the current node and call the “canReach” function for the nodes which are not visited yet.

 

Here is the algorithm:

 

  • canReach function:
    • If node is equal to ‘x’
      • Return true.
  • Vis[node] = 1.
  • Traverse the adjacency list of the current node “node” (say iterator ‘i’)
    • If adj[node][i] is not visited
      • if( canReach( adj [node][i], x, adj, vis) ) , if ‘x’ is found
        • Return True.
  • Return false.

 

  • given function:
    • Declare a 2-d vector “adj” for storing the adjacency list of all the nodes.
    • Declare a vector “vis” for marking nodes visited.
    • Create an adjacency list. This can be done by running a loop where ‘i’ ranges from 0 to ‘M’-1 and for each ‘i’ push EDGES[i][0] in list ADJ[EDGES[i][1]] and EDGES[i][1] in list ADJ[EDGES[i][0]].
    • Return canReach(source, destination, adj, vis)
Time Complexity

O(N + M), where ‘N’ is the number of nodes and ‘M’ is the number of edges.

 

 DFS takes O(N + M) times and creating an adjacency list will also take O(N + M) times, Thus overall time complexity will be O(N + M).

Space Complexity

O(N + M),  where ‘N’ is the number of nodes and ‘M’ is the number of edges. 

 

Extra space used by adjacency list ‘ADJ’ is of size O(N + M), and recursion stack, list ‘VISITED’ use O(N) space, Thus overall space complexity will be O(N + M).

Code Solution
(100% EXP penalty)
Find if Path Exists in Graph
Full screen
Console