Path In A Tree

Moderate
0/80
profile
Contributed by
53 upvotes
Asked in companies
FacebookMicrosoftAmazon

Problem statement

You are given a binary tree with ‘N’ number of nodes and a node ‘X’. Your task is to print the path from the root node to the given node ‘X’.

A binary tree is a hierarchical data structure in which each node has at most two children.

Example: 
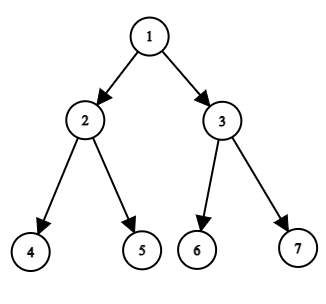
Here, for ‘X ’= 7, the output will be 1 3 7.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains an Integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow. 

The first line of each test case contains the elements of the tree in the level order form separated by a single space. If any node does not have a left or right child, take -1 in its place. Refer to the example below. 

The second line of each test case contains a single integer ‘X’, denoting the value of the node you have to find.
Example: 
Elements are in the level order form. The input consists of values of nodes separated by a single space in a single line. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image would be :


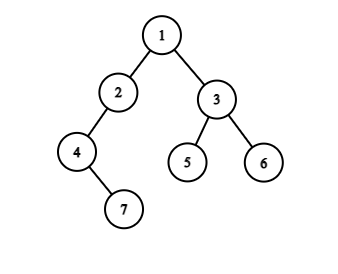
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null (-1).

Note: The above format was just to provide clarity on how the input is formed for a given tree. 

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format : 
For each test case, print a list of integers denoting the path from the root to the node ‘X’.

Output for each test case will be printed in a separate line.
Note : 
You do not need to print anything, it has already been taken care of. Just implement the given function.

No two nodes in the tree have the same data values.

You can assume that there always exists a node with data value ‘X’ in the given tree.
Constraints: 
1 <= T <= 10
1 <= N <= 10000
1 <= X <= N
All the node values will be in a range from 1 to N.

Time limit: 1 sec.
Sample Input 1 :
2
1 2 3 4 5 6 7 -1 -1 -1 -1 -1 -1 -1 -1
7
3 2 1 -1 -1 -1 -1
1
Sample output 1 :
1 3 7
3 1
Explanation For Sample Output 1:
For the first test case, the tree will be:


Here, for ‘X ’= 7, the output will be 1 3 7.


For the second test case, the tree will be:


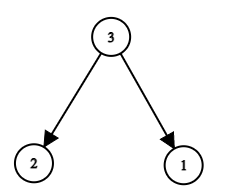
Here, for ‘X ’= 1, the output will be 3 1.
Sample Input 2 :
2
1 3 -1 -1 4 2 -1 -1 -1
1
4 -1 1 2 -1 -1 3 -1 -1
1
Sample output 2 :
1
4 1
Hint

Can you make a recursive function that traverses the different paths in the binary tree?

Approaches (1)
Recursive Approach

Let’s first define a function isPresent(temp, x, ans) where “temp” is the current node we are at, ‘x’ is the required value which we have to find, “ans” is the vector that stores the path.

 

This function returns “true” if ‘x’ is found in the subtree of it otherwise it returns false.

 

So, the idea is to traverse the whole tree from top to bottom while traversing if the function “isPresent” returns “true” then we insert the node into our “ans” vector otherwise not.

 

At last, we have “ans” vector which stores a path from the node whose value is ‘x’ to the root but we want the path from the root to the node so we just reverse the “ans” vector, and finally return it.

 

Here is the algorithm:

 

  • isPresent function:
    • If temp is equal to NULL
      • return false
    • If temp->data is equal to ‘x’
      • Return true.
    • If isPresent(temp->left, x, ans) returns true
      • Insert temp->left->data into “ans” vector.
    • If isPresent(temp->right, x, ans) returns true
      • Insert temp->right->data into “ans” vector.
    • Return false.
       
  • given function:
    • Declare a vector “ans” which has to be passed by reference in the “isPresent” function.
    • isPresent(root, x, ans).
    • Reverse the “ans” vector.
    • Return “ans”.
Time Complexity

O(N), where ‘N’ is the number of nodes in the tree.

 

In the worst case, we have to traverse the whole tree. Therefore, the overall time complexity will be O(N).

Space Complexity

O(N), where ‘N’ is the number of nodes in the tree.

 

As we are using a vector that stores the path from the root to the node which can take at most ‘N’ nodes. Therefore, the overall space complexity will be O(N).

Video Solution
Unlock at level 3
(75% EXP penalty)
Code Solution
(100% EXP penalty)
Path In A Tree
Full screen
Console