Points Visible

Hard
0/120
profile
Contributed by
1 upvote
Asked in company
NVIDIA

Problem statement

You are standing at a point in the coordinate plane facing east. You are given an array of points ‘points’, you are also given an integer ‘angle’ i.e. your field of view and while standing on the given you are allowed to rotate but not move. Your task is to determine the maximum number of points visible to you simultaneously.

Suppose you rotate ‘d’ degrees counterclockwise.

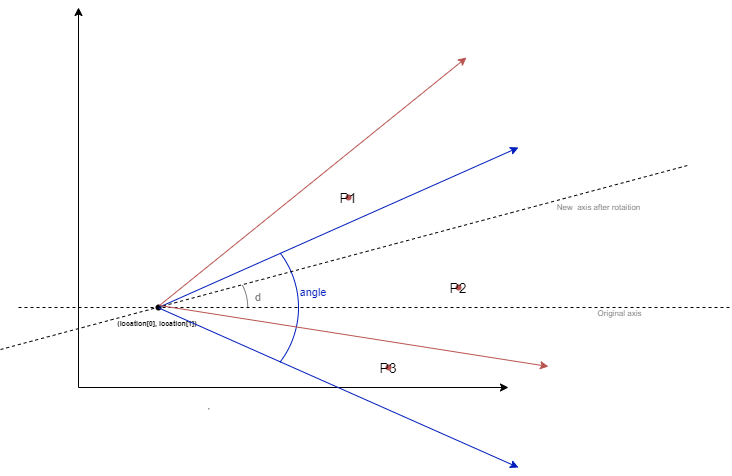
PointDiagram

For Example: 
You are given ‘location’ = [2, 2], ‘points’ = [[3,3], [4, 2], [3, 1]], ‘angle’ = 60. Due to the field of view only two, only 2, points [[2, 4], [3, 2]] simultaneously, are visible from the given position hence the answer is 2.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains a single integer ‘T’ representing the number of test cases.

The first line of each test case contains 2 space-separated integers, ‘N’, ‘angle’, where N represents the number of points in the given array and ‘angle’ is the given integer.

The second line of each test case contains two space-separated integers ‘x’ and ‘y’ representing coordinates of the location you are standing on.

The next ‘N’ lines of input contain two space-separated integers ‘a’ and ‘b’ representing ‘X’ and ‘Y’ coordinates of the points in the ‘points’ array.
Output Format: 
For each test case, print a single integer representing the maximum number of points visible at a time.

Print a separate line in each test case.
Constraints: 
1 <= T <= 10
1 <= N <= 10^5
0 <= angle <= 360
0 <= x, y, a, b <= 1000
Note : 
You do not need to print anything. It has already been taken care of. Just implement the given function.
Sample Input 1:
2
3 60 
2 3
3 3
3 1
1 1
2 40
1 1
0 1
2 1
Sample Output 1:
2
1
Explanation:
For the first test case, ‘location’ = [2, 3], ‘points’ = [[3,3], [3, 2], [1, 1]], ‘angle’ = 60. Due to the field of view only 2 points [[3, 3], [3, 2]] simultaneously are visible from the given position. Hence the answer is 2.

For the second test case ‘location’ = [1, 1], ‘points’ = [[0, 1], [2, 1]], ‘angle’ = 40 and ‘d’ = 90. Here only one either [0, 1] or [2, 1] is visible at once. Hence the answer is 1.
Sample Input 2:
2
3 10
0 0
3 4
2 3
4 0
2 50
1 1
2 5
0 0
Sample Output 2:
2
1
Hint

Try converting the points in radians

Approaches (1)
Sliding Window on Points

In this approach, we will draw a line from where we are standing to each point and find the angle the line makes with the X-axis and store it in the array. Then we sort the array according to the angle.

To find the angle of point(Px, Py) from our standing coordinate(A, B) we use the formula:

  • tanθ =  (Py - B) / (Px - A)

 

We can then start a sliding window of size ‘angle’ from the starting of the array. The maximum number of points in the sliding window will be the answer.

Here we will extend the sorted array with itself, with all the angles in the latter half will be increased by 2*π. 

 

Algorithm:

  • Create an empty array sortedAngles
  • Set sameLocation as 0
  • Iterate point through points
    • If point.x is equal to location.x and point.y is equal to location.y, Increase sameLocation by 1 and continue the loop
    • Set pointAngle as tan inverse of (point.y - location.y) / (point.x - location.x)
    • Insert pointAngle in sortedAngles
  • Sort the sortedAngles array
  • Add 2*π to all the values in sortedAngles and insert them back in the sortedAngles array
  • Set left and solution as 0
  • Iterate right from 0 to length of sortedAngles - 1
    • While sortedAngles[right] - sortedAngles[left] less than angle*pi / 180
      • Increase left by 1
    • Set solution as the maximum of itself and (right - left + 1)
  • Return solution + sameLocation
Time Complexity

O(N*log(N)), Where N is the size of the array 

 

We are sorting all the angles and iterating over them in a sliding window which will cost O(N*log(N)) time. Hence the final time complexity is O(N*log(N)).

Space Complexity

O(N), Where N is the size of the array

 

We maintain an array of 2*N. Hence the final space complexity is O(N)

Code Solution
(100% EXP penalty)
Points Visible
Full screen
Console