Problem
Submissions
Hints & solutions
Discuss
Print All The Nodes At Distance K From The Given Node
Moderate
0/80
Average time to solve is 20m
11 upvotes
Asked in companies



Problem statement
You have been given a Binary Tree of distinct integers and two integers “target” and ‘K’. You are supposed to return the list of values of all the nodes which are situated at ‘K’ distance from the target node.
Distance between two nodes ‘u’ and ‘v’ is defined as the number of edges in the shortest path from ‘u’ to ‘v’.
Note :You may assume that the given target node definitely exists in the given binary tree.
For the given binary tree
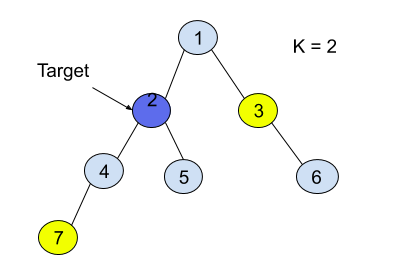
Nodes in the above binary tree that has K = 2 distance from the target node are highlighted in yellow colour.
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases are as follows.
The first line of each test case contains elements of the tree in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.
The second line of each test case contains two integers “target” and ‘K’ which are described above.
For example, the input for the tree depicted in the below image would be :
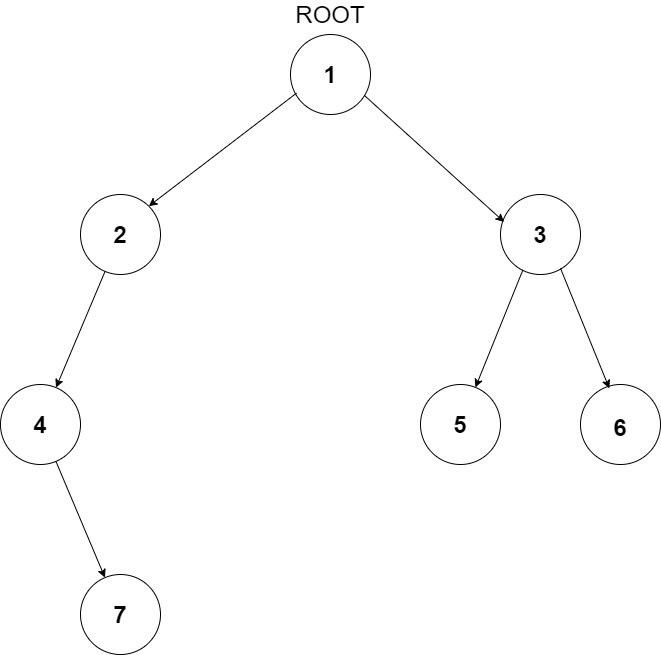
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation :
Level 1 :
The root node of the tree is 1
Level 2 :
Left child of 1 = 2
Right child of 1 = 3
Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6
Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)
Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null(-1).
The above format was just to provide clarity on how the input is formed for a given tree.
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Print a list of space-separated integers that denote the values of nodes that are at ‘K’ distance from the “target” node.
For each test case, print the output in a separate line.
You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints :
1 <= T <= 100
0 <= N <= 3000
0 <= data <= 10^4
0 <= target <= 1o^4
1 <= K <= 3000
Where ‘N’ is the total number of nodes in the binary tree, and “data” is the value of the binary tree node.
Time Limit: 1sec
Sample Input 1 :
4 5 -1 6 7 -1 -1 -1 -1 -1 -1 -1
2 2
1 2 3 -1 -1 -1 -1
1 1
4 3 -1 -1 -1
3 1
Sample Output 1 :
3 7
2 3
4
Explanation of Sample Input 1 :
The tree of the first test case is shown below.

For the first test case, there are two nodes {3, 7} which are at ‘K’ = 2 distance from the target node.
For the second test case, there are two nodes {2, 3} which are at ‘K’ = 1 distance from the target node.
For the third test case, 4 is the only node that is at ‘K’ = 1 distance from the target node.
Sample Input 2 :
2
2 4 -1 5 -1 -1 -1
2 2
1 4 2 -1 -1 -1 3 -1 -1
4 3
Sample Output 2 :
5
3
Explanation of Sample Input 2 :
For the first test case, 5 is the only node that is at ‘K’ = 2 distance from the target node.
For the second test case, 3 is the only node that is at ‘K’ = 3 distance from the target node.
Hint
Hint 1
Can you think of breaking down the problem into the sub-problems?
Approaches (1)
Approach 1
Efficient Approach
The basic idea of this approach is to divide the set of nodes into two groups:
- Nodes that are present in the subtree are rooted at the target node.
- Rest of the nodes.
For any node which is present in the subtree rooted at the target node, we can very easily find the list of node values that are at ‘K’ distance from the target node.
Let us assume a function
getNodesAtDistance(TreeNode<int> *root, int K, vector<int> &nodes)
Which finds the list of values of nodes present in the subtree rooted at the root node situated at ‘K’ distance from the root node. And “nodes” is passed as a reference to store the list of values. We can do a preorder traversal and get all those node values.
And for the rest of the nodes(not present in the subtree), observe that the shortest path will certainly pass through one of the ancestors of the target node. Let's say we are currently considering all the nodes for which the shortest path passes through an ancestor node( say “curAncestor”). And let say “curAncestor” is at a distance ‘T’ from the target node. Now we need all the nodes that are present in the subtree rooted at “curAncestor” (either left or right subtree which doesn’t contain target node) situated at ‘K’ - ‘T’ distance from the current ancestor node.
We should do the same thing for all ancestor nodes.
Let’s define another recursive function
int getNodes(TreeNode<int> *root, int target, vector<int> &nodes)
which returns the distance of the target node from the root node(returns -1 if the target is not present) and stores the nodes which are at ‘K’ distance from the target node.
Consider the following steps :
- If the current node is the target node, then we should add nodes that are at ‘K’ distance in the subtree rooted at the current node and return 0.
- Check if the target node is present in the left branch of the current node and it is so, then get the distance between the current node and target node and store it in a variable “leftDistance”.
- Now, look for the node in the right branch of the current node at ‘K’ - “leftDistance” - 2. We can easily get this using the getNodesAtDistance() function.
- If the target node is present in the right branch of the current node, proceed similarly (mentioned in step 2).
- Now if the target node is not present in either branch of the current node, return -1.
Time Complexity
O(N), Where ‘N’ is the number of nodes in the given binary tree.
Since we are doing a pre-order traversal and not visiting the nodes of the binary tree more than once. So the overall time complexity will be O(N).
Space Complexity
O(N), Where ‘N’ is the number of nodes in the given binary tree.
Since we are doing a recursive tree traversal and in the worst case (Skewed Trees), all nodes of the given tree can be present in the call stack. So the overall space complexity will be O(N).
Code Solution
(100% EXP penalty)
Print All The Nodes At Distance K From The Given Node
C++ (g++ 5.4)
Console
