Print Leaf Nodes

Easy
0/40
Average time to solve is 33m
22 upvotes
Asked in companies
SamsungDirectiAmazon

Problem statement

Given a binary tree, write a function that returns a list containing all the leaf nodes of the binary tree in the order in which they appear from left to right. In case two leaf nodes are at the same distance from the leftmost node, the one that has a lesser depth has to be printed first.

 Remember/Consider: 
If both horizontal and vertical distances are the same for two leaf nodes, then print the one with smaller node data.
Detailed explanation ( Input/output format, Notes, Images )
Input format : 
Elements in the level order form. The input consists of values of nodes separated by a single space in a single line. In case a node is null, we take -1 on its place.

For example, the input for the tree depicted in the below image would be :

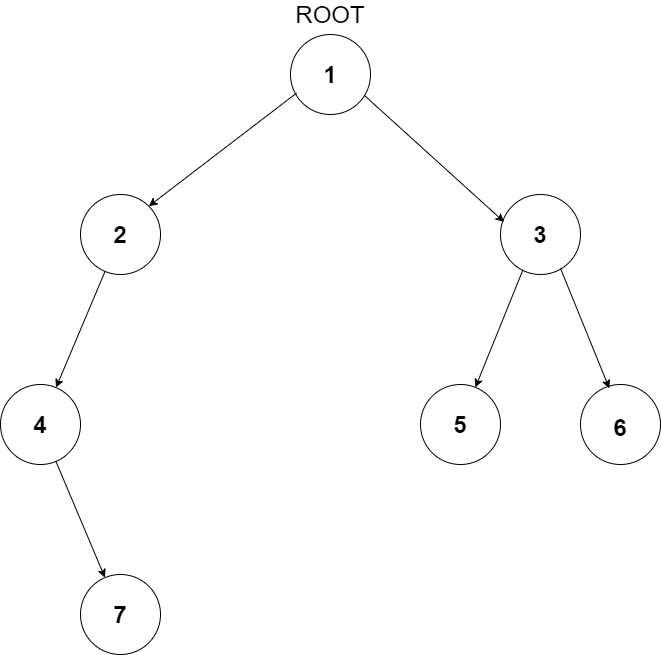
alt text

1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :

Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null (-1).
Note : 
The above format was just to provide clarity on how the input is formed for a given tree. 
The sequence will be put together in a single line separated by a single space. Hence, for the above depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format : 
You have to return a list containing all the leaf nodes of the binary tree in the order in which they appear from left to right.
Constraints : 
0 <= N <= 10^5
0 <= Value of node <= 10^8
Where 'N' is the total number of nodes in the BinaryTree.

time Limit: 1sec
Sample Input 1 :
8 3 10 1 6 -1 14 -1 -1 4 7 13 -1 -1 -1 -1 -1 -1 -1
Sample Output 1 :
1 4 7 13
Sample Input 1 :
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Sample Output 1 :
7 5 6
Hint

Think around vertical traversal of the tree!

Approaches (1)
Vertical Order Traversal

We will maintain the horizontal level of each node. The horizontal level of the root node is considered to be zero. Whenever we go to the left child of any node, its horizontal level is said to be one less than that of the parent node. Whereas, whenever we go to the right child of any node, its horizontal level is said to be one more than that of the parent node. To start with, we :- 

  1. Make a dfs traversal on the tree while maintaining the horizontal level and the vertical depth and a list that stores Triplets of the node's value, its horizontal level, and its vertical level
  2. We add the current node to the list only if it's a leaf node
  3. In case the current node is not a leaf node, we traverse further on to its children. For the left child, the horizontal level is the horizontal level of the current node minus one and the vertical level is vertical level of the current node plus one. Similarly, for the right child, the horizontal level of the right child is the horizontal level of the current node plus one and the vertical level is the vertical level of the current node plus one.
  4. If the current node is null, we simply return without doing anything.
  5. After the traversal is done and we have our list filled, we are going to sort the list according to the required conditions
  6. Then we are going to iterate through this list from start to end to copy only the node's value (not the levels) to a different list called ‘ret’.
  7. Finally, we'll return ‘ret’
Time Complexity

O(N)

Where N is the total number of nodes in the binary tree. We

Space Complexity

O(N)

Where N is the total number of nodes in the binary tree.

Code Solution
(100% EXP penalty)
Print Leaf Nodes
Full screen
Console