Query And Matrix

Moderate
0/80
Average time to solve is 50m
profile
Contributed by
9 upvotes
Asked in companies
Deutsche BankBarclaysDBS Bank

Problem statement

You are given a binary matrix with ‘M’ rows and ‘N’ columns initially consisting of all 0s. 'Q' queries follow. The queries can be of 4 types:

Query 1: 1 R index
Query 2: 1 C index 
Query 3: 2 R index
Query 4: 2 C index

In each query, the first input is the type of the query, the second input is whether we have to consider the row ('R') or the column ('C') and the third input is the index of the row/column. 

For each type 1 query, we need to flip the elements of the row/column having the given index. 

For each type 2 query, we have to output the number of zeros present in the row/column having the given index.
Note: 
Note that the matrix is a binary matrix, meaning that it only contains either 0 or 1.
Example : 
Given M = 3, N = 3, 
Queries : 1R1, 1R2, 2C1

So, in the above example the change in the matrix would look like this:

Example

Next query 2C1 will return the count of the number of zeroes in the 1st column: 1
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains an integer ‘T’ which denotes the number of test cases.

The first line of each test case contains two space-separated integers ‘M’ and ‘N’, denoting the dimensions of the matrix.

The next line contains a single integer ‘Q’ denoting the number of queries.

The next ‘Q’ lines of each test contain the queries.
Output Format: 
For each test case, return a single integer denoting the number of zeroes according to the given query of type 2.

Print the output of each test case in a separate line.
Note: 
You don’t need to print anything; It has already been taken care of. Juts implement the given function.
Constraints: 
1 <= T <= 10
1 <= M, N  <= 100
1 <= Q <= 1000
1 <= R <= M
1 <= C <= N
type = 1, 2

Time limit: 1 sec
Sample Input 1:
2
3 3
3
1R1
1R2
2C1
2 2
1
2R1
Sample Output 1:
1
2
Explanation of Sample Output 1:
In test case 1, Next query 2C1 will return the count of the number of zeroes in the 1st column: 1

The change in the matrix after the first and second queries would look like this:

Example

In test case 2, all the matrix elements are zero and hence the count of zeroes will be 2 for the first row.
Sample Input 2:
2
3 3
4
2C1
1R1
1R1
2R1
2 2
5
2C1
1R1
1R1
1R1
2R1
Sample Output 2:
3 3
2 0
Explanation of Sample Output 2:
In test case 1, 

First query 2C1 will return the count of the number of zeroes in the 1st column: 3

Next query 2R1 will return the count of the number of zeroes in the 1st column: 3

The change in the matrix after the second and third queries would look like this:

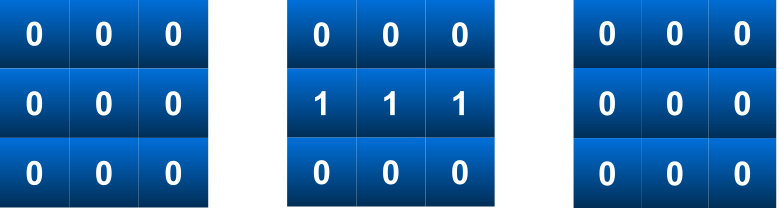
Example

In test case 2,

First query 2C1 will return the count of the number of zeroes in the 1st column: 2

Next query 2R1 will return the count of the number of zeroes in the 1st column: 0

The change in the matrix after the second and third queries would look like this:

Example

Hint

Can you think of traversing the given row or column?

Approaches (1)
Brute Force

A simple idea is to traverse the given row or column. If you come across a query that is of type 1 then swap 0 with 1 and vice-versa and for the query of type 2 initialize a variable ‘COUNT’ and increment count when you encounter ‘0’ and return ‘COUNT’.

 

The steps are as follows:

 

  • If the type of query is 1.
    • If we have to consider row ‘R’ at the given ‘INDEX’
      • Run a loop for row ‘INDEX’  and every column -  ‘i’ : 0 to ‘M’ - 1
        • Flip element at ‘MAT[ ‘INDEX’ ] [ ‘i’ ]’.
    • If we have to consider column ‘C’ at the given ‘INDEX’
      • Run a loop for every row and column ‘INDEX’ ’ - ‘i’ : 0 to ‘N’ - 1.
        • Flip element at  â€˜MAT[ ‘i’ ] [ ‘INDEX’ ]’.
  • If the type of query is 2.
    • Initialize a variable 'COUNT’ with 0.
      • If we have to consider row ‘R’ at the given ‘INDEX’
        • Run a loop for row ‘INDEX’ and every column -  i : 0 to ‘M’ - 1
          • If ‘MAT[ ‘INDEX’ ] [ i ]’ is ‘0’, Increment ‘COUNT’.
      • If we have to consider column ‘C’ at the given ‘INDEX’
        • Run a loop for every row and column ‘INDEX’  - i : 0 to ‘N’ - 1.
          • If ‘MAT[ i ] [ ‘INDEX’ ]’ is ‘0’, Increment 'COUNT’.
    • Return ‘COUNT’
Time Complexity

O(Q * max(M, N)), Where ‘Q’ is the number of queries and ‘N’ and ‘M’ are dimensions of the matrix.

 

Since we will be required to traverse through a single row and single column. So, the complexity is (Q * max(M, N)).

Space Complexity

O(1)

 

Since constant extra space is needed, so the overall space complexity will be O(1).

Code Solution
(100% EXP penalty)
Query And Matrix
Full screen
Console