Remove Edges

Moderate
0/80
Average time to solve is 20m
1 upvote
Asked in companies
UberFacebook

Problem statement

You are given an undirected graph with ‘N’ vertices and ‘M’ edges. Each edge has a particular type as described below:

An edge with type 1 can only be traversed by a person ‘A’.

An edge with type 2 can only be traversed by a person ‘B’.

An edge with type 3 can be traversed by both persons ‘A’ and ‘B’.

Your task is to determine the maximum number of edges that can be removed such that after removing these edges, all the nodes can still be traversed by both ‘A’ and ‘B’.

Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains an integer ‘T’, which denotes the number of test cases to be run. Then, the ‘T’ test cases follow. 

The first line of each test case contains two space-separated integers, ‘N’, denoting the total number of nodes, and ‘M’, denoting the total number of edges. 

Then ‘M’ lines follow. Each of which has three space-separated integers, ‘X’ ‘Y’, and ‘Z’.

‘X’ denotes the type of edge. ‘Y’ and ‘Z’  denote the two nodes between which the edge is present.
Output Format: 
For each test case, print a single line containing a single integer denoting the maximum number of edges that can be removed.

The output for each test case will be printed in a separate line.
Note: 
You do not need to print anything. It has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 10
1 <= N,M < 10 ^ 4
edges[i].length = 3
1 <= edges[i][0] <= 3
1 <= edges[i][1], edges[i][1] <= N

Where ‘T’ is the number of test cases, ‘N’ is the total number of nodes, ‘M’ is the total number of edges and edges[i] describes the i-th edge

Time Limit: 1 sec.
Sample Input 1:
1
4 6
1 3 4
1 1 2
2 1 3
2 2 4
3 1 4
3 2 3
Sample Output 1:
2
Explanation for sample input 1:

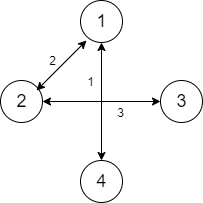
graph_example 

In the first case, there are a total of 2 typeA edges. One of them can be removed as the graph will still be traversable. Similarly, one of the two typeB edges can be removed as well because even after removing an edge, B can still visit all nodes using any other path. So, a total of 2 edges can be removed, and all nodes can still be visited by both ‘A’ and ‘B’.
Sample Input 2:
1
4 3
1 1 4
2 1 2
3 2 3
Sample Output 2:
-1
Explanation for sample input 2:

graph_example 

In this case, there is a path for ‘A’ between node 1 and node 4. There is also a path between node 2 and node 3. But there is no connection between these two paths. Hence ‘A’ can never visit all nodes. 
Similarly, for ‘B’, there is a path between node 1 and node 2. There is also a path between node 2 and node 3. But there is no path to reach node 4, and thus, there is no connection between node 4 and any other node. Hence ‘A’ can never visit all nodes.
Hint

Build the network instead of removing extra edges.

Approaches (1)
Using Find-Union Approach

Approach

The approach is to use Union-Find to find out the minimum number of edges that are required to make the graph a single connected component for both ‘A’ and ‘B’. Since using an edge of type 3 can minimize the total number of edges needed, we will consider these first. Finally, after considering all the edges, if the entire graph can be traversed by both A and B, we print the number of edges that were not needed, else we print “-1”.

Steps

  1. Define a class UnionFind and create two objects of it, typeA(N) and typeB(N), where N is the number of nodes.
  2. Initialize a variable addedEdges = 0 to store the count of edges that were added in order to make the graph traversable for both A and B.
  3. Run a loop from i=0 to i=edges.size() and do:
    1. Define edgeType = edges[i][0].
    2. Define node1 = edges[i][1] and node2 = edges[i][2].
    3. Since we are considering edges of type3 first, if(edgeType!=3) continue.
    4. Now, if node1 and node2 are not connected either by type1 edge or by type2 edge, we connect these nodes by a type3 edge and increment the counter. Formally, if(typeA.ifNotConnected(node1,node2) or typeB.ifNotConnected(node1,node2) addEdges++.  
  4. Now, again run a loop from i=0 to i=edges.size() and do:
    1. Define edgeType = edges[i][0].
    2. Define node1 = edges[i][1] and node2 = edges[i][2].
    3. If edgeType==1 and typeA.ifNotConnected(node1,node2), addEdges++.
    4. If edgeType==2 and type2.ifNotConnected(node1,node2), addEdges++.
  5. Now, if typeA and typeB both have a singly connected component, then return the number of edges that were not required, which is equal to edges.size - addedEdges.
  6. Else, return “-1”.

 

class UnionFind {

  1. Initialize a vector say component to keep track of which node belongs to which component.
  2. Initialize a variable say numOfComponents to store the number of total distinct components.
  3. Create a constructor UnionFind(n) {
    1. numOfComponents = n.
    2. For all i=0 to i=n, push i in component.
  4. findComponent(a) {
    1. if(component[a] != a) component[a] = findComponent(component[a])
    2. Return component[a].
  5. ifNotConnected(node1, node2) {
    1. If both nodes belong to the same component, i.e if(findComponent(node1) == findComponent(node2)) return false.
    2. Else connect them by making component[findComponent(a)] = b.
    3. Decrease numOfComponents by one and return true as they are connected.
  6. singlyConnected() {
    1. If numOfComponents == 1, return true.
Time Complexity

O(M), where  ‘M’ is the total number of edges.

 

The time complexity is O(M) because there are a total of ‘M’ edges, and for each edge, we are checking if this edge is required or not.

Space Complexity

O(N), where ‘N’ is the total number of nodes.

 

We need extra linear space to keep track of which nodes can be traversed by A and which nodes can be traversed by B.

Code Solution
(100% EXP penalty)
Remove Edges
Full screen
Console