Remove a node from BST

Moderate
0/80
Average time to solve is 15m
profile
Contributed by
18 upvotes
Asked in company
Qualcomm

Problem statement

You are given a BST (Binary search tree) with’ N’ number of nodes and a node ‘X’ (which is definitely present in the input the BST). You need to remove the node ‘X’ and return the root of the updated BST.

For example:

1 1

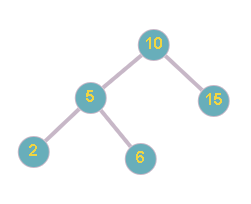
Figure1 : Input BST and Figure2: Output BST

In the above example, For the given BST (Fig.1) and X = 6,  we have output( Fig. 2 ) after removing node 6.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains an integer ‘T’, denoting the number of test cases. Then each test case follows.

The first line of each test case contains nodes in the level order form (separated by space). If any node does not have a left or right child, take -1 in its place.

The second and the last line of each test case contains ‘X’ denoting the node to remove.

For example, the input for the tree depicted in the below image.

1

10
5 15
2 6 -1 -1
-1 -1 -1 -1
Explanation : 
Level 1 :
The root node of the tree is 10

Level 2 :
Left child of 10 = 5
Right child of 10 = 15

Level 3 :
Left child of 5 = 2
Right child of 5 = 6
Left child of 15 = null(-1)
Right child of 15 =  null (-1)


Level 4 :
Left child of 2 = null (-1)
Right child of 2 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null(-1).
Note : 
The above format was just to provide clarity on how the input is formed for a given tree. 
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
 10 5 15 2 6 -1 -1 -1 -1 -1 -1
Output Format: 
For each test case, print a single line containing ‘N’-1 single space-separated integers, which is the inorder traversal of updated BST..

The output of each test case will be printed on a separate line.
Note: 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 5
1 <= N <= 5 * 10 ^ 3
1 <= nodeVal[i] <= 10 ^ 9

Time Limit: 1 sec.
Sample Input 1:
1
10 5 15 2 6 -1 -1 -1 -1 -1 -1
6
Sample Output 1:
2 5 10 15
Explanation of Sample Input 1:
In the first test case, the input figure is given above in the input format explanation. 
After removing 6 from BST, the tree becomes as below:

1

So the inorder traversal of the updated tree is: 2 5 10 15
Sample Input 2:
1
2 1 3 -1 -1 -1 -1
2
Sample Output 2:
1 3
Explanation of Sample Output 2 :

1 1

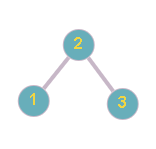
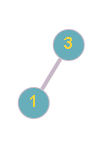
Figure1: Input BST  and Figure2: Output BST

So the inorder traversal of the updated tree is: 1 3
Hint

Consider nodes to be deleted as nodes with no child, only one child and two children separately.

Approaches (2)
BST Traversal

The deletion of a node in BST is based on the following three observations.

 

  • Node to be removed is the leaf node:
    • Simply remove the node.
  • Node to be removed has only one child:
    • Copy the child to the node and delete the child
  • Node to be deleted has two children:
    • Find in-order successor of the node. Copy contents of the inorder successor to the node and delete the inorder successor. (Note that in order predecessor can also be used.)
    • the inorder successor can be obtained by finding the minimum value in the right child of the node.

 

Algorithm :

 

    Let the ‘removeNode’ be the function to remove the given node from BST. It accepts two parameters (root node of tree, key node to be deleted). It returns the root of the updated tree.

 

  • If the root is NULL then return NULL
  • If the ‘key’ to be deleted is smaller than the ‘root -> val', then delete from left subtree by recursively calling the function with ‘root -> left' and ‘key’, store the return value in 'root -> left'.
  • If the ‘key’ to be deleted is greater than the ‘root -> val', then delete from the right subtree by recursively calling the function with ‘root’ -> right and ‘key’ and store the returned value in root -> right.
  • Else this ‘root’ node is the node to be deleted.
    • If the node has no child
      • Delete node and return NULL
    • If the node has an only right child
      • Store right subtree in ‘temp’ as ‘temp’  =  ‘root’  ->  right
      • Delete current node ‘root’
      • Return ‘temp’
    • If the node has only left child
      • Store left subtree in ‘temp’ as ‘temp’  =  ‘root’  ->  left
      • Delete current node ‘root’
      • Return ‘temp’
    • Else node has two children, find the inorder successor
      • Store the min node in ‘minNode’ by calling the function minRightNode as  ‘minNode’ = minRightNode( root -> right ).
      • Copy the content of ‘minNode’ to ‘root’ node as root->val = minNode ->val.
      • Recursively call removeNode on parameter root->right and minNode -> key to remove minimum value node from right subtree.
  • Return root

 

Description of minRightNode function:

 

 Let ‘minRightNode’ be the function that returns the minimum value node. It accepts the ‘root’ of the tree. Loop left down to find the leftmost node whose left child is NULL.

 

minRightNode( ‘root’ ):

  • While root left is not NULL
    • Move to left child i.e ‘root’ = ‘root’ - > left
  • Return root

 

Time Complexity

O (h),  where ‘h’ is the height of the tree.


 In the worst case, we may have to travel from the root to the deepest leaf node. If it is a skewed tree then ‘h’ becomes ‘N’. Hence the general time complexity is O(h)

Space Complexity

 O(h)  where ‘h’ is the height of the tree.

 

In the worst case, when the given BST is a skewed tree, height is equal to ‘N’, i.e. the number of nodes in the tree. Thus the recursion stack will take O(N) space. In general, it is O(h). 

Code Solution
(100% EXP penalty)
Remove a node from BST
Full screen
Console