Remove Nodes

Easy

0/40

Average time to solve is 15m

Contributed by

7 upvotes

Asked in company

Problem statement

Given a linked list such that each node represents a digit. Remove nodes at the 2^'I -th' position from the linked list where 'I' can be 0, 1, 2, and so on.

Detailed explanation ( Input/output format, Notes, Images )

Input format :

The first and only line contains the 'N' sized linked list elements separated by space and terminated by -1.

Output format :

The only line of output prints the updated linked list elements separated by a single space.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function and return the answer.

Constraints:

-10^9 <= 'data' <= 10^9

Time Limit: 1 sec

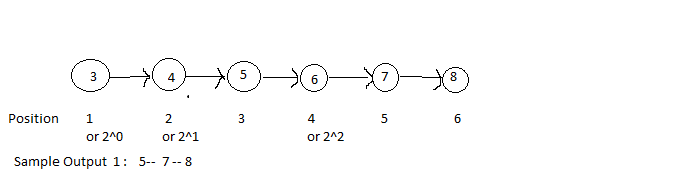
Sample Input 1 :

3 4 5 6 7 8 -1

Sample Output 1 :

5 7 8

Explanation For Sample Input 1:

Here the digits placed at the position with the power of 2 (1, 2, 4) will be removed. Hence the digits 3, 4, and 6 will be removed from the given list.

Sample Input 2 :

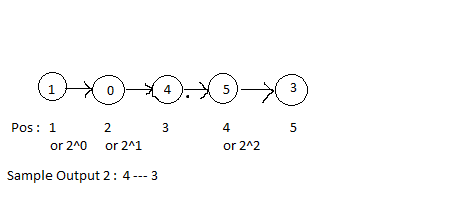
1 0 4 5 3 -1

Sample Output 2 :

4 3

Explanation For Sample Input 2 :

Here the digits placed at the position with the power of 2 (1, 2, 4)  will be removed. hence the digits 1, 0, and 5 will be removed from the given list.

Hint 1

Try to keep track of the position of the current node from head and skip nodes at the position of powers of 2.

Approaches (1)

Approach 1

Iterative

Try to traverse with updating the position of the current node from the head and if the position is in integral powers of 2 (use previous power of 2), then just skip that node and make a new link form the previous node to the next of the current node. Always irrespective of the size of the linked list you need to skip the head in the updated linked list.

Time Complexity

O(N), Where N is the size of the linked list.

As every node of the linked list is visited once for N nodes runtime complexity will be O(N).

Space Complexity

O(1)

As constant extra space, is used.

(100% EXP penalty)

Remove Nodes

Console