Reorder Edges

Moderate
0/80
Average time to solve is 30m
profile
Contributed by
6 upvotes
Asked in companies
AtlassianCoinDCXAmazon

Problem statement

You are given a connected directed acyclic graph of ‘N’ nodes and ‘N’ - 1 edges, such that there is only one edge between any two nodes. You can perform the below operation on the given graph zero or more times:

1) Choose two nodes, ‘X’ and ‘Y’, such that there exists an edge between ‘X’ and ‘Y’.

2) Change the direction of this edge, i.e., if this edge is directed from ‘X’ to ‘Y’, change the direction of this edge to be directed from ‘Y’ to ‘X’ and vice versa.

Your task is to reorder the edges of the given graph in such a way that there exists a directed path from each node to node 0, using the minimum number of operations.

Detailed explanation ( Input/output format, Notes, Images )

Input Format :

The first line of input contains an integer 'T' representing the number of test cases.

The first line of each test case contains a single integer, ‘N’, where ‘N’ denotes the total number of nodes in the given graph.

The next ‘N’ - 1 lines contains two space-separated integers, ‘U’ and ‘V’, where ‘U’ and ‘V’ represent the nodes that share a directed edge from ‘U’ to ‘V’.

Output Format :

For each test case, print the minimum number of operations required to make a directed path from each node to node 0.

The output of each test case will be printed in a separate line.

Constraints :

1 <= T <= 5
1 <= N <= 3000
0 <= U, V <= N - 1

Time Limit : 1sec

Note :

You do not need to print anything, it has already been taken care of. Just implement the given function.

Sample Input 1 :

2
4
0 1
0 2
1 3
5
1 0
2 0
3 1
4 1

Sample Output 1 :

3
0

Explanation Of Sample Input 1 :

Test Case 1 :  
The given graph is shown below.

1 

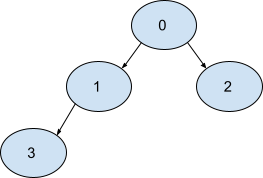
We can reverse edge 0 -> 1, 1 -> 3 and 0 -> 2. The resulting graph will be:

1

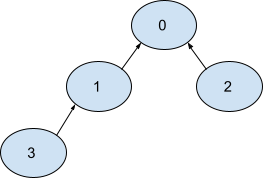
Now there exists a directed path from 1, 2, and 3 to 0 i.e., 1 -> 0, 2 -> 0, and 3 -> 1 -> 0 respectively.
So the minimum number of operations required will be 3.

Test Case 2 : 
The given graph is shown below.

1

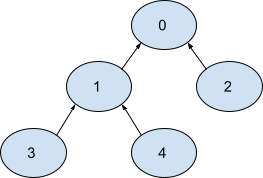
There is already a directed path from nodes 1, 2, 3, and 4 to 0 i.e., 1 -> 0, 2 -> 0, 3 -> 1 -> 0, and 4 -> 1 -> 0 respectively.
So the minimum number of operations required will be 0.

Sample Input 2 :

1
5
1 0
2 0
1 3
2 4

Sample Output 2 :

2

Explanation Of Sample Input 2 :

Test Case 1 :  
The given graph is shown below.

1

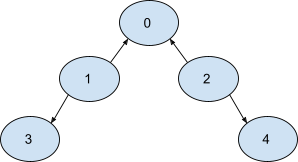
We can reverse edge 1 -> 3,  and 2 -> 4. The resulting graph will be:

1 

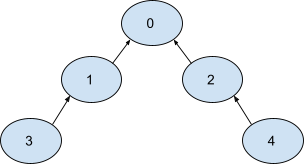
Now there exists a directed path from 1, 2, 3 and 4 to 0 i.e., 1 -> 0, 2 -> 0, 3 -> 1 -> 0, and 4 ->. 2 -> 0 respectively.
So the minimum number of operations required will be 2.
Hint

Convert the given directed graph into a bidirectional graph by adding reverse edges.

Approaches (2)
Depth First Search

The idea here is to convert the given directed acyclic graph into a bidirectional acyclic graph by adding reverse edges, i.e., for every edge present in the graph, we will add an edge with opposite direction.

 

For example: 

Below, the left side directed graph will be converted into the right side undirected graph.

The edges marked in red are reverse edges.

Then we will do a depth-first search from node 0 and count the number of edges that are not reverse edges.

 

Algorithm:

 

  • Declare a 2 - Dimensional array of integers, say ‘adjList’,  to store the adjacency list of the given directed graph.
  • Build the adjacency list using the edges array given in the problem.
  • Call the ‘depthFirstSearch’ function with node 0 and ‘adjList’ as arguments, and store its returned value in ‘answer’
  • Return ‘answer’

 

Description of ‘depthFirstSearch’ function

 

This function is used to traverse the given graph and count the number of non-reverse edges.

This function will take three parameters :

  • root: An integer denoting the root node.
  • parent: An integer denoting the parent node of the ‘root’ node.
  • adjList: A 2 - Dimensional array of integers denoting the adjacency list of the given graph with reverse edges.

int depthFirstSearch(root, parent, adjList):

  • Declare an integer ‘count’ to store the count of non-reverse edges.
  • Run a loop for ‘i’ from 0 to the size of adjList[root] - 1
    • Declare a integer say ‘currNode’ and initialize it with absolute value of  ‘adjList[root][i]
    • If  ‘currNode’ is not equal to ‘parent’
      • Call the ‘depthFirstSearch’ function with ‘currNode’, ‘root’, and ‘adjList’ as arguments, and add its returned value in ‘count’
      • If the edge ‘root’ -> ‘adjList[root][i]’ is not a reverse edge:
        • Increment ‘count’ i.e. do ‘count’ = count + 1 as we need to reverse it to make the path of the current node to node 0 valid.
  • Return ‘count’
Time Complexity

O(N), where ‘N’ is the total number of nodes in the graph.

 

Here, building the adjacency list will take O(N - 1) time since we have ‘N’ - 1 edges, and performing a depth-first search on the given graph takes O(N + N - 1) time. 

Hence, the overall time complexity will be O(N - 1) + O(2 * N - 1), which is O(N).

Space Complexity

O(N), where ‘N’ is the total number of nodes in the graph.

 

We are using an adjacency list that takes O(N - 1) space as we need to insert ‘N’ - 1 edges into the list. Moreover, we need O(N) extra space in the form of recursive calls for depth-first search when the given graph is bamboo or a one-sided tree. 
Hence, the overall space complexity will be O(N) + O(N), which is O(N).

Code Solution
(100% EXP penalty)
Reorder Edges
Full screen
Console