Problem
Submissions
Hints & solutions
Discuss
Serialize And Deserialize BST
Easy
0/40
Average time to solve is 15m
Problem statement
You are given a Binary Search Tree with its root node. You are supposed to serialize a binary search tree into a string and deserialize the string into a binary search tree.
Note :
Serialization is the process of converting an object into a stream of bytes.
Deserialization is the opposite process of creating an object from a stream of bytes.
You can apply your own serialization and deserialization algorithms.
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.
The first line of each test case contains elements in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.
For example, the input for the tree depicted in the below image will be:
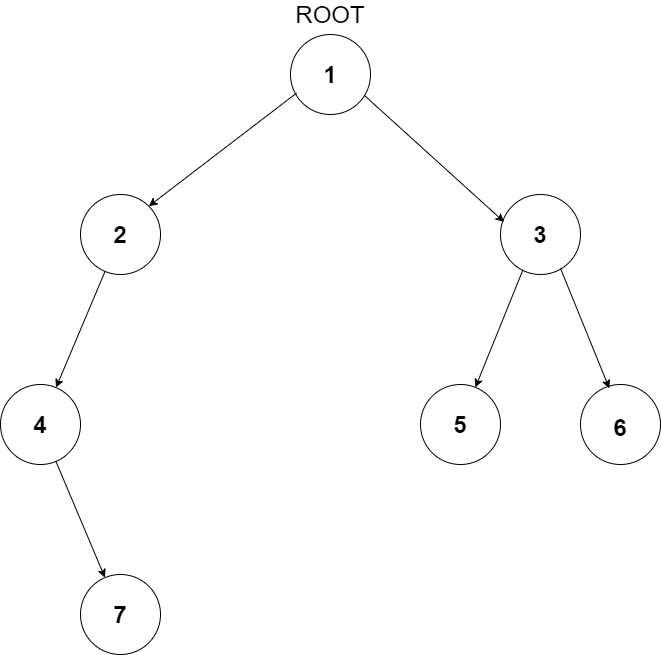
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation :
Level 1 :
The root node of the tree is 1
Level 2 :
Left child of 1 = 2
Right child of 1 = 3
Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6
Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)
Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null(-1).
The above format was just to provide clarity on how the input is formed for a given tree.
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Print the level order traversal of the Binary Search Tree after Deserialization separated by spaces. It should match with the level order traversal of the initially given tree.
Print the answer of each test case in a new line.
Note :
None of the pointers in the new tree should point to nodes in the original tree, otherwise, the expected output can be different.
You don’t have to print anything, it has already been taken care of. Just implement the given function.
Constraints :
1 <= T <= 50
1 <= N < 10^4
0 <= data < 10^4 and data!=-1
Time Limit: 1 sec
Sample Input 1 :
2
24 15 33 12 21 30 36 9 -1 18 -1 27 -1 -1 -1 -1 -1 -1 -1 -1 -1
15 9 21 7 13 19 23 5 -1 11 -1 17 -1 -1 -1 -1 -1 -1 -1 -1 -1
Sample Output 1 :
24 15 33 12 21 30 36 9 18 27
15 9 21 7 13 19 23 5 11 17
Explanation Of Sample Input 1 :
In the first test case, The values of the nodes are 24, 15, 33, 12, 21, 30, 36, 9, 18, and 27. After performing Serialization and Deserialization, the tree should remain the same. So, the level order traversal of the tree is 24, 15, 33, 12, 21, 30, 36, 9, 18, and 27.
In the second test case, The values of the nodes are 15, 9, 21, 7, 13, 19, 23, 5, 11, and 17. After performing Serialization and Deserialization, the tree should remain the same. So, the level order traversal of the tree is 15, 9, 21, 7, 13, 19, 23, 5, 11, and 17.
Sample Input 2 :
2
1 2 3 -1 -1 -1 -1
25 16 34 13 22 31 37 -1 -1 -1 -1 -1 -1 -1 -1
Sample Output 2 :
1 2 3
25 16 34 13 22 31 37
Hint
Hint 1
Hint 2
Can we separate the node values with space for serialization and separate those for deserialization?
Approaches (2)
Approach 1
Approach 2
Post-Order Traversal
The idea is to perform a recursive Preorder traversal and store the node values in a string separated by spaces. Here we are utilizing the property of the binary search tree, if we do a pre-order traversal of a binary search tree, we’ll get sorted values. For deserialization, first, create the left sub-tree, then create the right sub-tree and then return the root node.
The steps are as follows:
Serialization:
- Define an empty string ‘serialized’ for storing the serialized string.
- Define a recursive function ‘preOrderTraversal’, which takes two arguments root node of the tree, and the final string, ‘serialized’.
- If the root is null, then return from the function.
- If the size of the string is not zero ie. any value is already pushed into the string, then add a space in the string.
- Now, convert the node value into a string(using to_string in C++) and push it into the string ‘serialized’.
- Recursively call ‘helperForDeserialization’ for the left and the right sub-tree.
- Return ‘serialized’ as the final answer.
Deserialization:
- Here, we will use a string stream(for C++)(stringstream helps divide the string separated by spaces, commas, etc).
- Define an empty array ‘allValues’, which stores all the node values of the tree from the given string.
- The first step is to break the string into the node values using stringstream. It takes the given string, an empty string, and space as its arguments. It separates all the strings present in the given string separated by spaces.
- A while loop is executed with the condition getline( It is a standard library function that reads a string or a line from the input stream).
- Push the string into the vector ‘allValues’ by converting it into an integer.
- Initialize an integer ‘index’ to 0, which denotes the position that we are currently in the ‘allValues’ array.
- Define a recursive function ‘helperForDeserialization’ which four arguments ‘allValues’, ‘index’, ‘minValue’, ‘maxValue’ which denotes the array containing all the node values, index at which we are currently, minimum node value for the current subtree, and the maximum node value for the current subtree.
- Base Conditions are when the index is out of the index, or the current node value is not satisfying the binary search tree properties i.e check whether it lies in the range (minimum value, maximum value), if not then return NULL.
- Make a tree node using the allValues[index] as the current root node.
- Recursively call the function ‘helperForDeserialization’ for the left and the right subtree by incrementing the index and after changing the maximum and the minimum values for the left and the right subtree.
- Return the ‘root’ as the answer to the current subtree.
- Return the node returned by the function ‘helperForDeserialization’ as the answer.
Time Complexity
O(N ), where N is the total number of nodes in the given binary search tree.
As we are visiting every node exactly once. Hence, the time complexity is O(N).
Space Complexity
O(N), where N is the total number of nodes in the given binary search tree.
As we are having a function calling stack that stores at most all the nodes of the binary search tree and a string that stores the serialized form of the binary search tree. Hence, the overall space complexity is O(N).
Code Solution
(100% EXP penalty)
Serialize And Deserialize BST
C++ (g++ 5.4)
Console


