Single Source Shortest Path

Easy
0/40
profile
Contributed by
34 upvotes
Asked in company
InfoEdge India Private Limitied

Problem statement

You are given an undirected graph with 'N' nodes and 'M' edges. The weight of each edge in the graph is one unit.


Given a source vertex 'src', you must return an array 'answer' of length 'N', where 'answer[i]' is the shortest path length between the source vertex 'src' and 'i'th vertex.


Note: 
All the nodes are zero-based.
Example: 
Input:
N=5, M=5, edges=[(0, 1), (1, 4), (2, 3), (2, 4), (3, 4)], src=1 
Output: 1 0 2 2 1

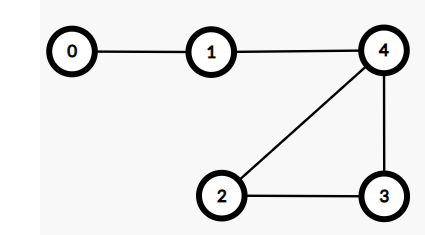
alt.txt

Explanation: The path from vertices are:-
(1->0) = 1 -> 0, path length is 1.
(1->1) = 1 -> 1, path length is 0.
(1->2) = 1 -> 4 -> 2, the path length is 2.
(1->3) = 1 -> 4 -> 3, path length is 2.
(1->4) = 1 -> 4, the path length is 1.
Hence we return [1, 0, 2, 2, 1]
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of the input will contain integers 'N' and 'M', denoting the number of nodes and the number of edges.

The next 'M' lines contain two space-separated integers, denoting an undirected edge between 'a' and 'b'. 

The next line contains an integer denoting 'src'.
Output Format:- 
The only line contains 'N' space-separated integers, i.e., the path length to each node.
Note:- 
You don't need to print anything. Just implement the given function.
Sample Input 1:
4 3
0 1
0 3
2 3
0
Sample Output 1:
0 1 2 1
Explanation Of Sample Input 1:
For test case one:
Input:
N=4, M=3, edges=[(0, 1), (0, 3), (2, 3)], src=0 
Output: 0 1 2 1

Explanation: The path from vertices are:-
(0->0) = 0 -> 0, path length is 0.
(0->1) = 0 -> 1, path length is 1.
(0->2) = 0 -> 3 -> 2, path length is 2.
(0->3) = 0 -> 2, path length is 1.
Hence we return [0, 1, 2, 1]
Sample Input 2:
3 3
0 1
1 2 
0 2
2
Sample Output 2:
1 1 0
Constraints:
1 <= N, M <= 10^2
0 <= src, edges[0], edges[0] <= N-1
Time Limit: 1 sec
Hint

Perform DFS for each of the nodes.

Approaches (3)
DFS

Approach: 

  • The brute force algorithm for finding the shortest path in an undirected graph with unit distances exhaustively checks all possible paths between two given vertices and selects the shortest one.
  • Here is the step-by-step algorithm for each node:
    • Initialize a variable ‘minimumLength’ to store the shortest path found.
    • For each pair of vertices (‘start_vertex’, ‘end_vertex’) in the graph, do the following:
      • Initialize an empty list ‘currentLength’ to store the current path being explored.
      • Use a depth-first search (DFS) algorithm to find all possible paths between ‘start_vertex’ and ‘end_vertex’. During the DFS, maintain a visited array to avoid cycles.
      • For each path found during the DFS, compare its length to the value of ‘minimumLength’. If the ‘currentLength’ is shorter, update ‘minimumLength’ to the ‘currentLength’.
    • Once all pairs of vertices have been processed, ‘minimumLength’ will contain the shortest path in the graph.
    • Insert the value of ‘minimumLength’ in the ‘answer’ array.
  • Return the ‘answer’ array.

 

Algorithm:

 

Function void DFS(int node, int dest, int[][] adjacencyList, int &minimumLength, int currentLength):

  1. If ‘node’ equals ‘dest’:
    1. Update ‘minimumLength’ with a minimum of ‘minimumLength’ and ‘currentLength’.
    2. Return
  2. Mark ‘visited[node]’ as true.
  3. For each ‘i’ in ‘adjacencyList[node]’:
    1. If ‘visited[i]’ is not visited:
      1. DFS(‘i’, ‘dest’, ‘adjacencyList’, ‘minimumLength’, ‘currentLength’+1)
  4. Mark ‘visited[node]’ as false.

 

Function int[] shortestPath(int n, int[] edges, int src):

  1. Initialize an ‘answer’ array of length ‘N’ with 0.
  2. Iterate over the edges and create the ‘adjacencyList’ for the graph.
  3. For ‘node’ from 0 to ‘N’-1:
    1. Initialize an integer variable ‘minimumLength’ with a verge large integer value and ‘currentLength’ with 0.
    2. Initialize an empty boolean array ‘visited’ with false.
    3. Call DFS(‘node’, ‘src’, ‘adjacencyList’ ‘minimumLength’, ‘currentLength’, 0)
    4. ‘answer[i]’=’minimumLength’
  4. Return ‘answer’

 

Time Complexity

O( N*(N+M) ), Where ‘N’ is the number of nodes and ‘M’ is the total edges in the graph. 

 

For each vertex in the graph, we are doing a DFS, which takes O(N+M) time in the worst case. Hence the total time complexity is O(N*(N+M)).

Space Complexity

O( N ), Where ‘N’ is the number of nodes in the graph. 

We are taking O( N ) extra space. Hence, the overall space complexity will be O( N ).

 

Code Solution
(100% EXP penalty)
Single Source Shortest Path
Full screen
Console