SJF

Easy
0/40
Average time to solve is 20m
profile
Contributed by
30 upvotes
Asked in company
Flipkart limited

Problem statement

You have to implement the shortest job first scheduling algorithm.


Shortest Job First is an algorithm in which the process having the smallest execution(burst) time is chosen for the next execution. Here, you will implement a non - preemptive version (a process will wait till process(es) with shorter burst time executes). You have to return the average waiting for the given number of processes.


Completion Time: Time at which process completes its execution.


Example: 

SJF will schedule the job which is having least burst time.

Hence, Average waiting time = (5 + 0 + 2) / 3 = 2.33

Detailed explanation ( Input/output format, Notes, Images )

Input format :

The first line contains a single integer 'N' which represents the number of processes.

The next 'N' lines contains two space-separated integers ‘at’ and ‘bt’ which represent arrival time and burst time for the 'ith' process, respectively.

Output format :

Print a floating value of 2 decimal points that represent average waiting time.

Note:

You don’t have to print anything; it has already been taken care of. Just implement the given function. 

You have to return the answers up to two decimal places.

Sample Input 1 :

3
0 3
0 1
0 2

Sample Output 1 :

1.33

Explanation For Sample Input 1:

The table for the given number of processes is 


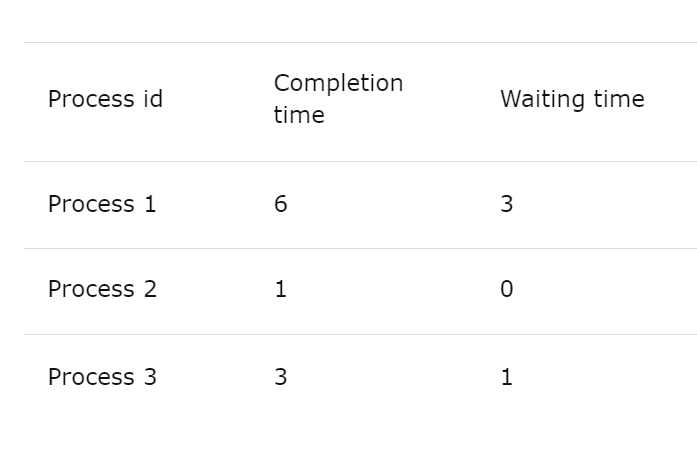
Therefore, the average waiting for the given process is 1.33.

Sample Input 2 :

2
1 4
1 3

Sample Output 2 :

1.50

Constraints:

1 <= N <= 10^2
1 <= at, bt <= 10^3

Where 'N' denotes the number of processes, 'at' and 'bt' represents the arrival time and burst time of any process.

Time Limit: 1 sec.
Hint

Can you think of choosing the shortest job first?

Approaches (1)
Constructive Approach

The idea is to use the definition of the SJF. That is, first keep track of the process with the minimum arrival time because it will come first and then keep track of the process with the minimum burst time among the arrived process.

 

  1. To keep track of the waiting times, completion times, turn around times and the process which has been executed, we will create arrays waitingTime, completionTime, turnAroundTime, and completed respectively.
  2. Run a loop for the total number of processes, that is until all processes are executed.
    • In each iteration, check for the minimum arrival time process and with the minimum burst time .
    • After finding the process, execute it. Means,update turnAroundTime[i] = completionTime[i] - arrivalTime[i] and completionTime[i] = turnAroundTime[i] - burstTime[i] as mentioned in the formulas above and put this process as completed in the completed array i.e. completed[i] = true.
  3. Consider the remaining processes and repeat the above steps for each of them.
  4. Finally, calculate the average turn around and average waiting time and return both of them in an array.
Time Complexity

O(N ^ 2), where 'N' denotes the number of processes.

 

Since we are executing all the N processes and then for  each process, we are checking for the minimum arrival and burst time of all the processes, i.e. we are iterating all the remaining processes in each iteration of outer loop. Therefore, total time complexity will be O(N) * O(N) = O(N ^ 2).

Space Complexity

O(N), where ‘N’ denotes the number of processes.

 

Since we are creating new arrays to store all the waiting times, turn around times, completion times, completed processes. So, the net space complexity will be 4 * O(N) = O(N).

Code Solution
(100% EXP penalty)
SJF
Full screen
Console